数学の分野一覧　詳細編～中学・高校数学から大学数学へ。こんな応用があります。

前回の記事の続きです。

この記事では、数学の分野を広く浅く紹介していきます。

中学・高校数学で学んでいるのはどんな分野なのか？
大学数学はどんな分野があるのか？
どんな応用があるのか？

など、数学の全体を見渡せるような記事にします。
中学生・高校生を対象にしていますが、大学数学についても広く触れています。
かなり分量が多いので、気になる箇所をつまみながら見てもらえるとうれしいです。

前回の振り返り

前回の記事では、数学の分野の一覧を載せました。

ざっくり振り返ると次の分野があります。

• 幾何学

• 解析学

• 代数学

• 集合論

• 確率論・統計学

• 整数論

• グラフ理論・離散数学

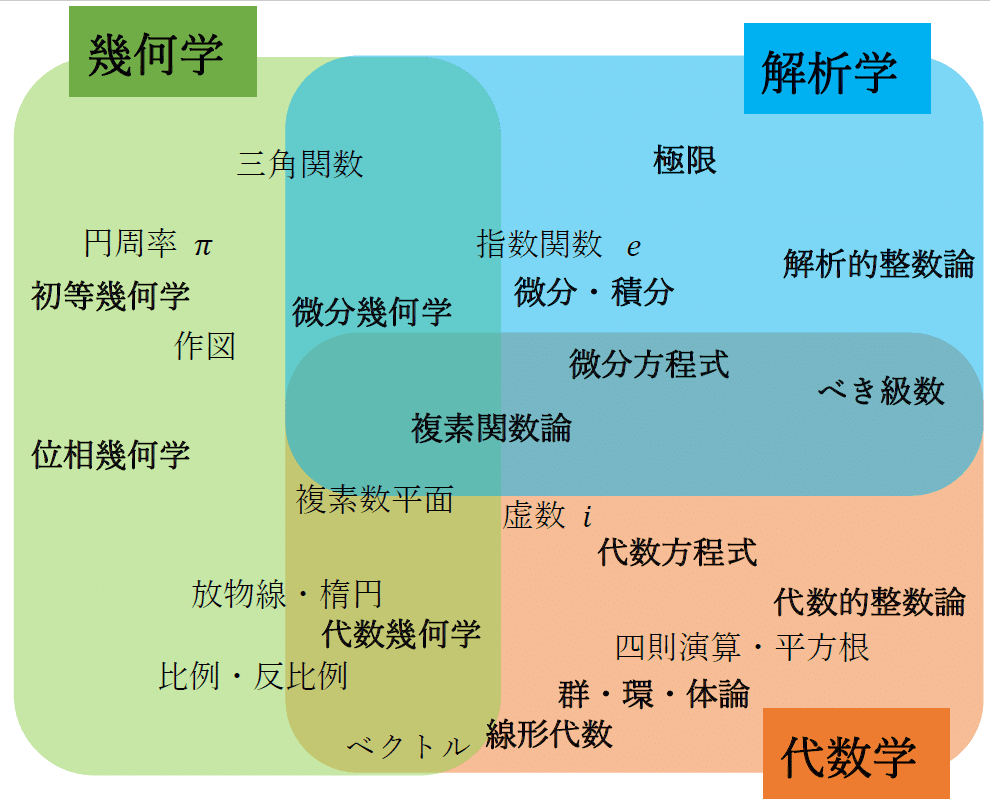
これだけでもたくさんありますが、さらに細分されます。
ここからは、一つ一つ深ぼってみていきましょう。

分野の数が多いため、興味のあるところだけ見てもらえれば大丈夫です。

また、最後におまけも載せているので、もし良ければ見てください。

幾何学

幾何学とは、図形を対象に調べる分野です。
古くから、土地の測量に用いられてきており、かなり歴史が古いです。また、幾何学的な模様など、図形自体の美しさに魅了される人もいるようです。

初等幾何学

初等とは、「素朴」といった意味合いがあります。
作図問題や合同・相似な図形、円周角などは、中学～高校で習うと思います。また、三角比（sin, cos, tan ）や円周率（$${\pi}$$）なども有名です。

古くから測量に用いられてきました。例えば、山の高さや川幅のような直接測れない距離を求めることができます。
最近では、「コンピュータによって、円周率を何兆桁まで求めた！」というニュースがあります。これは、円周率そのものよりも、コンピュータの性能を示したいという側面が強いらしいです。

位相幾何学

トポロジーとも呼ばれる分野です。
「マグカップとドーナツは同じ」というのは少し有名な話です。

硬く言うと「連続変形を考える」分野です。
例で説明すると

一本のひも持っていることを想像してください。
それをピンと張った状態と、弛ませた状態。どちらも同じひもですから、同じものと思えますよね。

もしも、ひもがゴム製なら、伸び縮みもできます。これが連続変形です。「図形があって、連続変形で別の図形ができたとしても、それは同じものと思う」というのがトポロジーの基本的な考え方です。

そのような意味で、「マグカップとドーナツは同じ」というわけです。

位相幾何学は、後述の微分幾何や代数幾何の土台となる分野でもあります。

微分幾何学

微分の力を使って、図形を調べようとする分野です。
やや解析的側面が強いため、詳しくは解析学の項で解説します。

代数幾何学

代数的な道具を使って、図形を調べる分野です。
こちらも、代数的な側面が強いため、詳しくは代数学の項で解説します。

複素数平面

複素数は、虚数 $${i}$$ と実数 $${a, b}$$ に対して、
$${a+bi}$$
で表される数のことです。複素数を表すことは、実数 $${a, b}$$ に対応しており、つまり、平面を考えることに対応しています。

特に、回転や拡大を表すのに便利で、コンピュータ内の計算で用いられています。 

解析学

高校数学の山場であり、難易度の高い解析学。ですが、現代において、かなり強力な道具であるのも事実です。

もともとは、物理現象を調べるために作られたもので、物理学者のニュートンが発明したと言われています。
現代においても、物理現象を表すのに必要不可欠な分野です。

極限

主に、数列と関数の極限の2種類があります。
例えば、「関数$${f(x)}$$の$${x}$$を$${a}$$に飛ばす」という言い方をして、

$$
lim_{x\to a} f(x)
$$

と書きます。$${a}$$は$${\infty}$$でもよく、例えば、

$$
lim_{x\to \infty}   x^2=\infty,
$$

$$
lim_{x\to 0}   1/x =\infty
$$

などが成り立ちます。
極限は微分・積分の定義に必要になります。

微分

微分を計算することは、”関数の変化率”や”グラフの接線の傾き"を求めることに対応しています。

物理現象では、ある現象の変化する様子がわかる場合が多いため、微分が必要になります。

例えば、「エアコンで部屋が冷える様子」を調べるとき、知りたいのは「室温」ですが、わかることは「どのくらい熱が移動するか」です。つまり、熱の移動量＝微分から室温を求めることになります。

積分

微分の逆の操作であり、グラフの面積を求めることに対応する操作です。

微分の項で説明した「熱の移動量（微分）から室温を求める」ためには、微分の逆の操作である積分を使えばいいことになります。

微分方程式

方程式の中に微分が入っているものを微分方程式と呼びます。
上述の通り、物理現象を表すのに使われます。有名なのは運動方程式です。

$$
F=ma
$$

言葉で書くと、（力）＝（重さ）＊（加速度）であり、加速度は「速度の微分」から得られるため、運動方程式は微分方程式の1つです。

例えば、コンピュータシミュレーションは、微分方程式を解くことで、現象を予測しています。

複素関数論

微分を複素数の範囲で考える分野です。初めは、よくわからないと思われますが、かなり便利であることが知られています。

複素数の範囲で微分できる関数を正則関数と呼びます。
例えば、正則関数であれば、テイラー展開（参照：べき級数）できることが知られています。（べき級数は比較的調べやすい）

べき級数

べき級数とは、次の形の無限和のことです。

$$
 \Sigma_{n=0}^\infty a_n x^n . 
$$

簡単な例だと等比級数があります。初項１で公比 $${r}$$ の等比級数の和は、

$$
\Sigma_{i=1}^n  r^{n-1} =\frac{1-r^n}{1-r} .
$$

これを無限に足す、つまり、$${n\to \infty}$$のとき、$${r < 1}$$ であれば、

$$
r^\infty \to 0
$$

$$
\frac{1-r^n}{1-r} \to \frac{1}{1-r}
$$

が成り立ちます。

べき級数は微分・積分ができる他、さまざまな性質があります。
また、関数をべき級数の形に表す（テイラー展開という）便利な操作があります。

フーリエ級数

べき級数では $${x^n}$$ の無限和でしたが、フーリエ級数では、代わりに

$$
sin(x), cos(x), sin(2x), cos(2x), sin(3x), cos(3x), …
$$

の無限和を考えます。

$${sin(x), cos(x)}$$ のような周期的な関数は、フーリエ級数に表すことで、より解析がしやすくなる場合があります。

解析的整数論

主に、微分の力を使って、整数を調べていく分野です。
特に、ゼータ関数が有名で、これは複素関数の知識が必要になります。
ゼータ関数には、素数の情報が含まれているとされ、有名な素数定理は、その重要な結果の一つです。
素数定理：「$${n}$$ 以下の素数は大体、$${\frac{n}{log(n)}}$$ くらいある」

極限の厳密な定義

$${\epsilon - \delta}$$論法と呼ばれる、極限の厳密な定義を与える理論です。

大学数学の難関の一つ、基本的に数学科の3年生が学ぶ内容です。
極限や微分などの厳密な定義を与えるもの。抽象的で難しいが、極限や微分について、厳密な証明ができる。

ちなみに、元々は「関数$${f(x)}$$の$${x}$$を$${\infty}$$に飛ばす」と言った、直感的な定義が、主に物理の分野で使われていた。しかし、困まること（直感に反すること）が見つかり、数学的に厳密な定義が必要になったらしい。

ルベーグ積分

こちらも大学数学の難関の一つ。基本的に数学科の3年生が学ぶ内容。
ルベーグ積分に対して、上記の積分はリーマン積分という。ルベーグ積分は、リーマン積分の拡張であることが知られている。

微分幾何学

微分の力を使い、図形を調べる分野です。多様体論とも呼ばれる。
図形の中でも、滑らかな形をしたもの、つまり、微分ができる図形を対象とします。

例えば、微分ができる曲線では、接線や曲線の長さを考えることができる。そのため、図形について、より深く調べることができる。

代数学

文字通り、”数の代わり”に変数や文字を使う分野です。代表的なのは、方程式や解の公式などです。
幾何学と同様、古くから方程式が利用されていたと言われています。

代数方程式

代数学で扱うのは、（多項式）＝０ の形をしている代数方程式です。
例えば、連立一次方程式や2次方程式は、中学～高校の範囲で習います。

解の公式のように、方程式を解く方法が目的となります。
例えば、コンピュータシミュレーションで微分方程式を解くのに、連立一次方程式を解く必要があります。

また、平方根 $${\sqrt{2}}$$ や虚数 $${i}$$ は、代数方程式（2次方程式）の解として定義されています。特に、虚数は、上述の通り、幾何学・解析学に応用されている重要な数です。

四則演算・数の拡張

四則演算や数は、どの分野でも出てきますが、代数学の側面があります。
例えば、四則演算を拡張したものは、後述する体論に対応しています。

数の拡張は、

自然数→整数→有理数→無理数→実数→虚数

のように、歴史的にどんどん多くの数が発明されてきました。
特に、ルート（根号）や虚数は、2次方程式の解として定義される数です。

これらの基本的な数は多くの分野で使われます。
虚数は、上述の複素数平面や複素関数など応用があります。

もっと身近な例だと、日常的に使うA3用紙やA4用紙などは、縦横の比率が
$$
1:\sqrt{2}
$$
として定義されています。

線形代数学

大学数学の一番初めに学ぶ科目です。抽象的なため、難しいと感じる人も多いようです。

線形代数は、連立一次方程式を解くために作られた概念です。
キーワードは、行列・ベクトルなど。

例えば、コンピュータシミュレーションや微分方程式への応用があります。

代数的整数論

整数論ですが、整数よりも広い概念を扱う分野で、整数方程式の解となる数（代数的数という）を調べる分野です。

逆に、代数的数ではない数を超越数と言うのですが、「どんな数が超越数か？」という基本的な問題は、かなり難しいものです。
ちなみに、虚数 $${i}$$ は代数的数ですが、円周率 $${\pi}$$ は超越数です。

群・環・体論

線形代数学のさらに一般化で、四則演算のような”演算”を考える分野です。
前述の代数的整数論・次項の代数幾何学に必要な分野になります。

代数幾何学

近年、発展している分野で、代数学の道具で幾何学（図形）を調べる分野です。

高校までだと、比例のグラフ（$${y=x}$$）や放物線($${y=x^2}$$)、円($${x^2+y^2=1}$$)などがあります。このように（代数）方程式で定義される図形を調べるのが代数幾何学です。

応用上は、暗号理論や学習理論（AIなど）など、意外な応用先があります。
また、整数論への応用もあり、有名なフェルマーの最終定理の証明にも、代数幾何学が使われています。

集合論

数学の全ての分野は、集合を調べる分野と言っても過言ではなく、それだけ基礎的な分野です。
集合論では、集合や写像（関数の一般化）について、基本的な性質を調べます。

基礎的であり、どの分野を学ぶにも必要な概念になります。

余談ですが、公理的集合論という「集合とは何か？」を真剣に考える分野があります。やや哲学的で難しすぎることで少し有名な分野です。

確率論・統計学

数学の中でも、現実に近いため、想像しやすい分野だと思います。
一方で、平均・分散・標準偏差など、多くの概念が登場するため、難しさを感じる人も多いです。

応用は、データ解析・ビックデータなどがあります。

最近では、情報化社会と呼ばれるほど、情報にあふれています。そのため、情報を解析するために、確率・統計は必須になります。

離散数学・グラフ理論

離散とは、連続の逆の意味です。例えば、整数のような、”飛び飛びの値”を対象とする分野です。

特に、グラフとは、頂点と辺から構成される対象です。ゲームや荷物の配送などを考えるために必要です。（例えば、頂点が配送拠点、辺が道路、と考えることができる）。

整数論

整数（1, 2, 3, …）を調べる分野で、解析的整数論・代数的整数論と対比して、初等整数論とも呼ばれます。

整数という基本的なものを調べるのは、実はかなり難しいです。
実際、証明には”テクニック”が必要で、体系的な理論や複雑な定義とは違う難しさがあります。
一方で、他の分野の知識を総動員して解かれる問題もあり、この分野が難しいとされる所以です。

上記の難しさの一方で、整数に面白さ・美しさを感じる人が多く、「数学の女王」とも呼ばれる分野です。

実は、暗号理論への応用が知られています。

おまけ～世界一美しい公式とは～

オイラーの公式

$$
e^{i\pi}=-1
$$

は、世界一美しい公式と言われています。

なぜ、美しいのか？

それは、いろいろな分野が混ざって、1つのシンプルな公式が成り立っているからです。
ざっくり言うと、虚数 $${i}$$ は代数学、円周率 $${\pi}$$ は幾何学、自然対数 $${e}$$ は解析学です。

最後に

このように、数学には多くの分野が存在し、しかも、それぞれが関わり合って、さらに発展しています。

みなさんの勉強しているのは、どの分野か？どんな応用があるのか？
そんな疑問が解消できたならうれしいです。

参考文献

1. 江戸の数学「第4章　実学としての和算」https://www.ndl.go.jp/math/s1/c7.html#:~:text=%E5%B9%BE%E4%BD%95%E5%AD%A6(geometry)%E3%81%A8%E3%81%AF,%E5%85%85%E3%81%A6%E3%81%9F%E3%82%82%E3%81%AE%E3%81%A7%E3%81%97%E3%81%9F%E3%80%82　（2022/07/22　閲覧）

2. 梅谷 武　「代数記号の歴史」
   https://pisan-dub.jp/doc/2011/20110114001/3_1.html#:~:text=%E4%BB%A3%E6%95%B0%E6%96%B9%E7%A8%8B%E5%BC%8F%E3%81%AE%E6%AD%B4%E5%8F%B2%E3%81%AF,%E3%81%90%E3%82%89%E3%81%84%E6%98%94%E3%81%AE%E3%81%93%E3%81%A8%E3%81%A7%E3%81%99%E3%80%82
   （2022/07/23　閲覧）

3. 文部科学省　「中学学習指導要領（平成29年告示）解説　数学編」https://www.mext.go.jp/component/a_menu/education/micro_detail/__icsFiles/afieldfile/2019/03/18/1387018_004.pdf

4. 文部科学省　「高等学校学習指導要領（平成30年告示）解説　理数編」https://www.mext.go.jp/content/1407073_05_1_2.pdf

5. 趣味の大学数学　「大学数学のロードマップ ～ 分野一覧と学ぶ順序」https://math-fun.net/20180711/412/　（2022/07/22　閲覧）

6. Wikipedia　「Portal:数学/分野」
   https://ja.wikipedia.org/wiki/Portal:%E6%95%B0%E5%AD%A6/%E5%88%86%E9%87%8E　（2022/07/22　閲覧）