
物理学と機械学習最前線2 [Ab-Initio Solution of the Many-Electron Schrödinger Equation with Deep Neural Networks]
この記事について
この記事は量子化学計算をDNNを使って行なったFermi Net[1]を、物理的な背景も含めて紹介します。
概要
この論文はDavid Pfauらによって、2019/5/27にarXivに投稿されました。この記事の概略は以下のようになります。
量子化学計算をニューラルネット(NN)で行うというFermi Netを提案。量子化学計算は波動関数の最適化をエネルギー最小化を介して行うが、波動関数の近似をNNが担っている。ハートリー・フォック近似、無限遠方の境界条件、反対称性など物理的な制約をかなり組み込んでおり、エネルギー計算も物理的な計算によって算出する。従来は系によって手法を変えなければならなかったがFermi Netはどの系でも良い結果を出せる。
Key Insight
この論文のポイントは以下の3つです。特に2番目の物理制約を入れるという思想は通常の物理計算でも一般的(エネルギー一定など)で、ニューラルネットを用いた研究でも同様のコンセプトはHamiltonian Graph Networks with ODE Integrators[2]などにもみられます。(以前の記事参照)
1. 量子化学計算の波動関数近似部分をNNが担う
2. 波動関数の反対称性、電子のスピン、無限遠方の境界条件などの物理制約を数多く含む
3. ハートリー・フォック近似の波動関数と一致するように事前学習を行う
物理的な背景(量子力学と量子化学計算)
物質の物理的な性質(電子状態など)を計算しようと思うと、電子の状態を記述する必要があります。そして電子のような小さいものの状態は、慣れ親しんでいる運動方程式では記述できず、量子力学というもの使う必要があります。

上図: ピン止め効果とマイスナー効果によって宙に浮かぶ磁石。この現象は量子力学なくして説明できない。 https://commons.wikimedia.org/w/index.php?curid=2911413
量子力学では、電子の状態を複素関数である「波動関数」で電子の状態を記述します。下の式はシュレディンガー方程式と呼ばれる量子力学の基本的な方程式で、波動関数とエネルギー(ハミルトニアン、右辺のHハット)の関係を示しています。ψが波動関数です。

このシュレディンガー方程式(と様々な近似に基いて)物質の電子状態を研究する物性物理学の分野に「第一原理計算」と呼ばれる物理シミュレーションがあります。
理論的にいえば、「原子番号とその構造の情報(結合の状態)さえあれば、実験結果から得られた経験パラメータがなくとも、物質の電子状態は記述できるはず」という第一原理の立場から、原子番号と物質の構造をもとに、物質の電子状態をシミュレーションします。
しかし、物質の状態を厳密に計算しようと思うと、物質中に存在しているアボガドロ数分(6x10²³)の電子同士の相関を計算する必要があります。現実的に不可能なので、実際には様々な近似を使います。その1つがこの論文の事前学習に用いているハートリー・フォック近似(スレーター行列式による近似)です。

シミュレーションの方法としては、その構造で最安定(エネルギーが最小)になる電子状態を逐次的に計算して求めます。なぜエネルギーを最小化する必要があるのかというのを直感的に説明すると、「エネルギーが低い=物質がその状態に落ち着いている確率が一番高い」だからです。
具体的に言うと、「電子状態を計算して、内部エネルギーを計算→エネルギーが小さくなるように電子状態を更新」を逐次的に繰り返してエネルギーが最小になる電子状態を探索します。

エネルギー最小化のイメージ図。エネルギーが高いと物質が安定して存在しない。逐次計算によって安定して物質が存在する状態(第一原理計算/量子化学計算だと波動関数)を求める
似たようなコンセプトで、分子の電子状態を計算をする量子化学計算があります。第一原理計算の主な計算対象は固体や表面状態であるのに対し、量子化学計算は主に分子を対象にしています。
この論文はこの量子化学計算とニューラルネットを組み合わせた研究です。
問題設定
基本的には量子化学計算ですが、この研究では波動関数の近似をNeural Networkに任せています。ニューラルネットを使ってもやることは一緒で、エネルギーの最小化です。
通常の量子化学計算では、以下のようにブラケット表記にしたハミルトニアンを最小化しています。

同じようにニューラルネットを用いた波動関数でも、同様に最小化をすることができます。

波動関数を近似するニューラルネット
Fermi Netの全体図は以下のようになっています。複数の原子核(位置R)と電子(位置r)を入力として、波動関数ψを出力しています。特徴的なのは、それぞれの電子-全原子核間相互作用、それぞれの電子-電子間相互作用を、対応させたまま伝播させている点です。
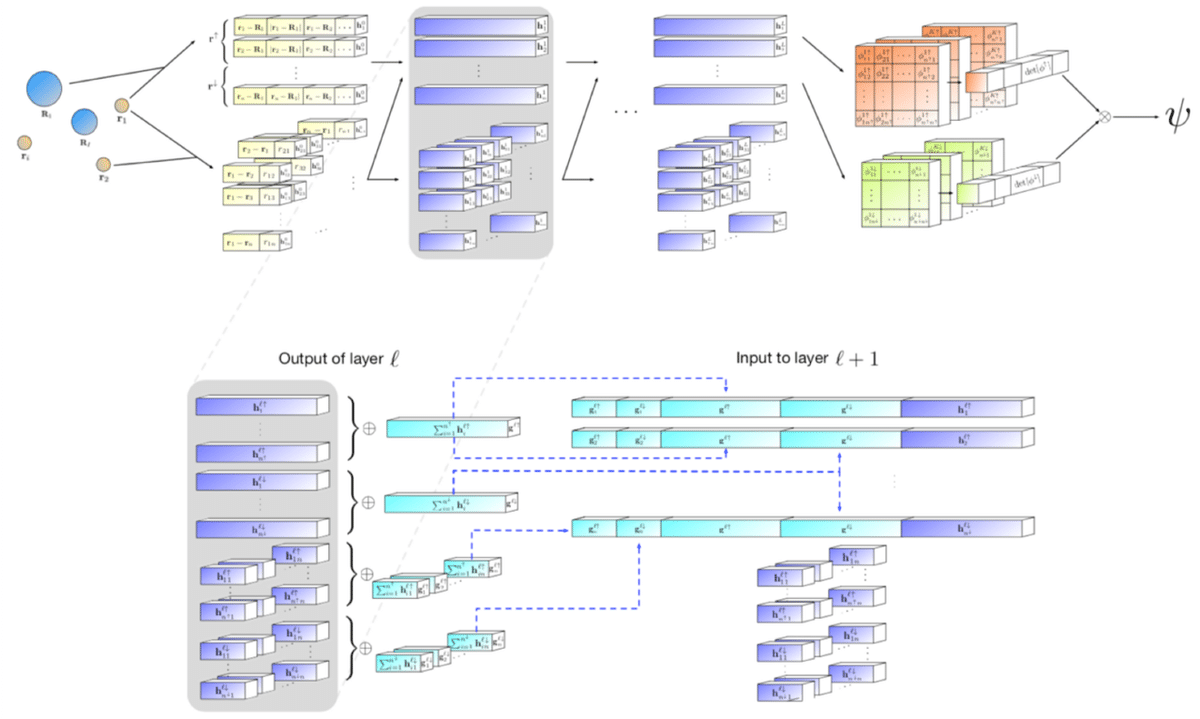
まず、入力層と第1中間層を拡大してみます。入力層は、上部の電子-原子核間相互作用を処理する部分と、下部の電子-電子間相互作用を扱うの2つに分かれています。

各相互作用を混ぜ合わせるのではなく、各相互作用の要素は保ったままで次の層に伝播させていることに注意してください。こうすることで、各相互作用と他の相互作用間の関係をニューラルネットで抽象化しつつψを構成しています。
また、電子-原子核間相互作用では、入力場所を固定することによって、間接的にネットワークに電子のスピンの情報を与えています。
次に、中間層の処理がどうなっているかを詳しくみてみます。下の図が中間層lから中間層l+1に伝播させるときの処理を示しています。大きく分けると和を取る前半パートと、中間層の構成を決める後半パートにわかれています。

前半の和を取るパートでは、スピン毎に処理をしていることに注目して下さい。上部の電子-原子核間相互作用の部分では、スピン↑電子-原子核間相互作用、スピン↓電子-原子核間相互作用毎に和をとっています。下部の電子-電子間相互作用の部分では、スピン↑同士、スピン↓同士で和をとっています。スピンによって電子の性質が異なるため、スピンによって処理を変えることで物理的な制約を加えています。
中間層の構成は下記のようになっています。下の式は電子iの中間層lの表現です。

上記の式のように、スピン毎に中間層の潜在表現の総和を結合したものを中間層の表現にしています。左からスピン↑の電子-原子核間相互作用の潜在表現の全電子総和、スピン↓の電子-原子核間相互作用の潜在表現の全電子総和、電子iとスピン↑の電子-電子間相互作用の潜在表現の総和、電子iとスピン↓の電子-電子間相互作用の潜在表現の総和、電子iの潜在表現、です。
次に最終層を見てみます。最終層は以下のようになっています。ここでは「電子の波動関数がdeterminantで表せる」「波動関数が無限遠方でゼロになる」という物理制約を加えています。

最終層は、最終中間層で計算された電子jが所属する波動関数φ_iに対して線形変換を加えた後、原子核mとの異方性を加味した減衰項の積をとって計算されます。

Wとgは重みとバイアス、πは異方性ありの減衰をコントロールする3x3の(学習可能な)パラメータ、αはスピン(↑or↓)、kは軌道の組み合わせを示しています。ここでexpの肩の項によって、「rが無限大になる(無限遠方)になると波動関数はゼロになる」という物理的な制約を課しています。
下図のdet φという部分は、先ほどのφ行列のdeterminant(行列式)をとるという操作を示します。詳細は省きますが、これは電子の波動関数の性質を物理制約として加えていることになります。電子をはじめとするフェルミオンという粒子は、電子の交換に対して反対称(入れ替えると符号が反転する)という性質があり、その性質を表現するためにdeterminantで波動関数を表現することがあります。ここで詳細は説明しませんが、気になる方は「アシュクロフト・マーミンの固体物理の基礎」等をご覧ください。ここでkは軌道の組み合わせのIDです。

その他の工夫
ADAM等のFirst orderの最適化手法ではなく、Second Orderの最適化手法であるKFACを改変したものを使っています。Second Orderの最適化手法は計算量の観点からあまり使われない印象がありますが、Fermi Netでは以下の通りADAMを圧倒する収束性を示しています。

また、固体物理における代表的な近似方法である「ハートリー・フォック近似」と波動関数が一致するように事前学習させたのちに、本学習を行なっているようです。


結果
以下の表は基底状態のエネルギーを計算した結果です。Fermi Netがかなり健闘しています。
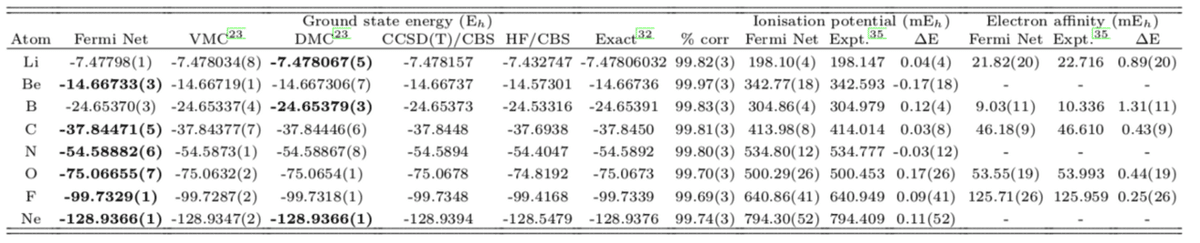
孤立分子の計算においても、従来手法のCCSD(T)と同等の成果をあげています。

次に、窒素分子のdissociation curveを計算した例です。UCCSD(T)では明らかに上手くいっていませんが、Fermi Netだと、MR-ACPFと同等程度の精度を出せています。

最後にH10 chainを計算した例です。下の弾は非常に精度が高いMRCI+Q+F12 CBSとの差分をとった図です。AFQMC CBSには及びませんが、Fermi Netはかなり高い精度を出しています。

この研究の影響
第一原理計算では、「第一原理」と言いながらも様々な近似を使い、最適な近似方法は系による、という現実があります。。さらにLDA+Uのように恣意的なパラメータも含まれていることもあります。この手法が発展すれば、系によらず汎用的な電子状態計算モデルができるかもしれません。
まとめ
量子化学計算において、波動関数の近似を Neural Networkで行うFermi Netを紹介しました。このFermi Netの良いところは、どの計算対象でも一貫して良い結果が出せるという点です。従来は計算対象によって、手法を変える必要がありましたが、Fermi Netを用いればそのような手間はなくなるかもしれません。
Reference
1. David Pfau et al.Ab-Initio Solution of the Many-Electron Schrödinger Equation with Deep Neural Networks, arXiv:1909.02487 (2019)
2. Alvaro Sanchez-Gonzalez et al. Hamiltonian Graph Networks with ODE Integrators. arXiv:1909.12790, 2019
---------------------------------------------------------
TwitterでMLの論文や記事の紹介しております。
https://twitter.com/AkiraTOSEI
記事は以上です。ここから下は有料設定になっていますが、特に何もありません。調査や論文読みには労力がかかっていますので、この記事が気に入って投げ銭しても良いという方がいましたら、投げ銭をして頂けると嬉しいです。
ここから先は

Akira's ML news & 論文解説
※有料設定してますが投げ銭用です。無料で全て読めます。 機械学習系の情報を週刊で投稿するAkira's ML newsの他に、その中で特に…
記事を書くために、多くの調査や論文の読み込みを行っております。情報発信を継続していくためにも、サポートをいただけると非常に嬉しいです。
