自然界を書き表す記号(sign)～微分の世界～

　ニュートンやライプニッツが微分を記号として表現して以来、数学・物理・工学を習う上で必須科目となった。

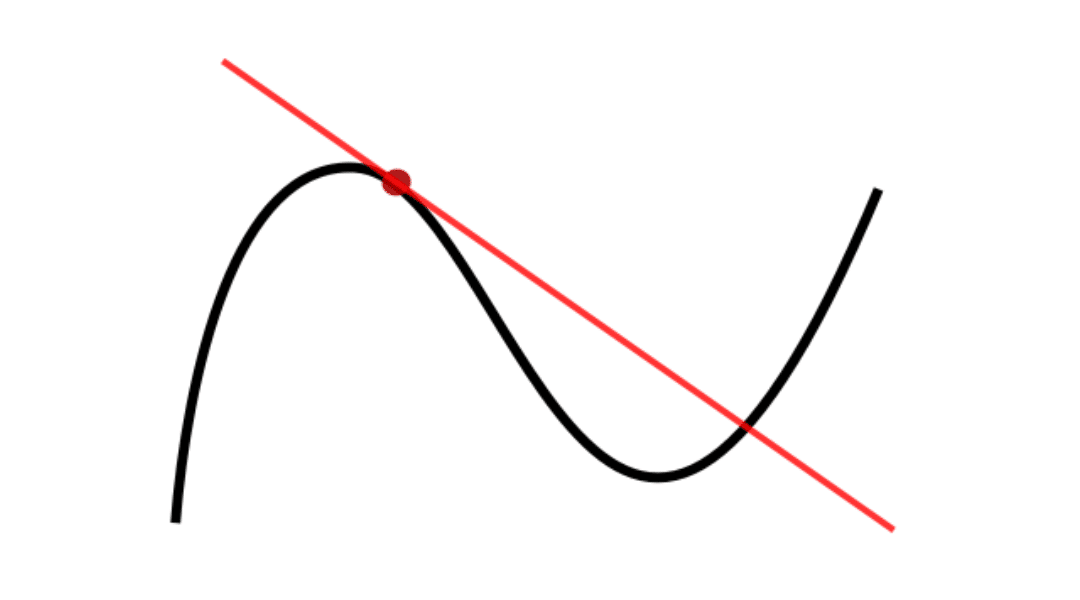
　図で見たら分かるように、要するに接線である。

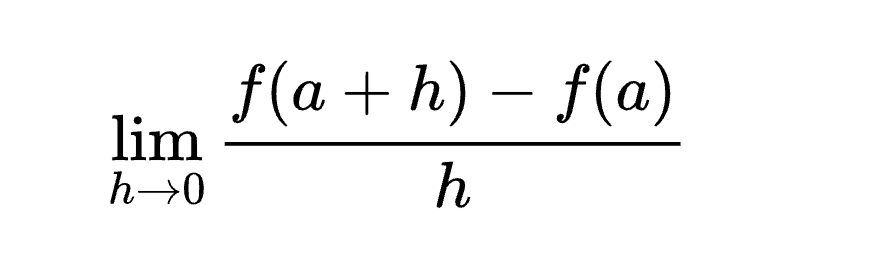
　この式がある関数を微分にする公式だ。

　極限を理解せずして、微分の本質を理解出来ずである。

　この式から分かる通りある関数の2点があり、1点であるf(a+h)をf(a)に寄せて行くという意味だ。

　そうすれば、図上では接線になる。

　図では理解しやすいが、ここで詰まりやすいのは式の形だ。

　分母分子とも0に近づくとどうなるというのか。

　ここで極限の考え方が登場する。分母分子が0になる。つまり0/0の形になる。ということは不定形になるのだ。

　不定形だとそのまま極限に飛ばすことが出来ない。これが重要なのだ！

　なぜならこれから極限を出来る形に直す必要が出てくるからだ。

　例えば、

　という関数を立てたとする。そして極限として極限式に代入して解くと、

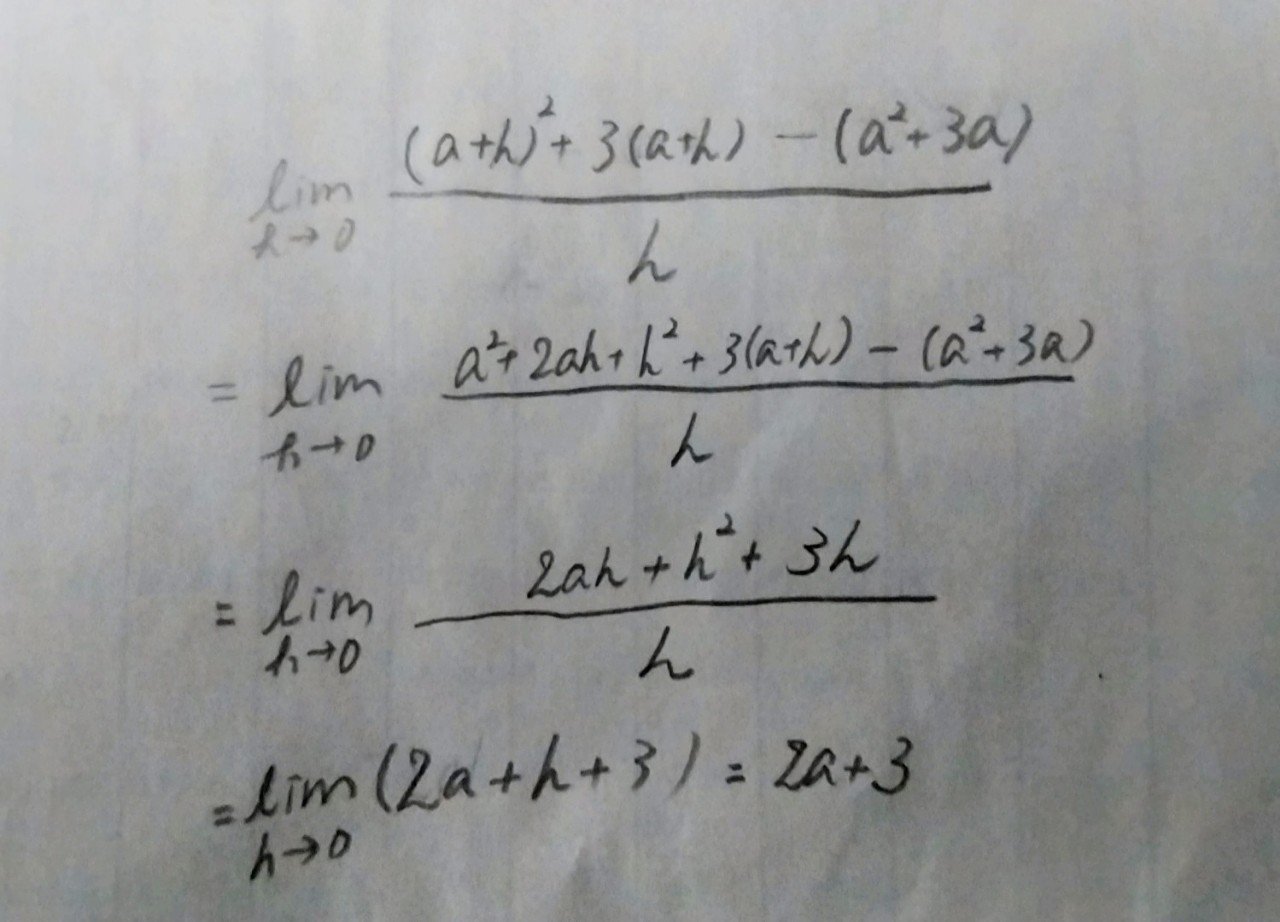
　となる。

　aは定数なので、これを連続の意味を込めて変数のxに直すことが出来る。

　つまりf(x)＝2x+3となるのだ。

　これによりある関数の接点が出た。そしてこれを応用して時間という概念を用いることにより、距離を時間微分して速度を出し、さらに微分すると加速度が出る。

　つまりこれで自然の様々な運動や図形を記述することが出来るようになるのだ。