
python(tkinter)で簡単な電卓を作ろう #基礎編
今回はtkinterで簡単な電卓を作っていきます。最終的には機能を多めにして関数電卓のような感じにしますが、今回は基礎編として四則演算と累乗ができるようにしていきます。
*今回はtkinterで作りますが、少しプログラムをいじればPygameなどでもできると思います。
電卓のやり方と仕組み
さて、Pythonでは$${\verb|"1 + 2"|}$$そのまま文字列を計算式として入力したのでは計算できません。しかし、int関数やfloat関数に入力したのではエラーを吐くだけです。
これを解決してくれる便利な組込関数がPythonにはあります。それが$${\verb|eval|}$$関数と$${\verb|exec|}$$関数です。これの違いは、eval関数は値を返すのに対し、exec関数は値を返さずただ実行するだけという点です。これだけ聞くとexec関数が無能に見えますが、この関数はeval関数と違い複数行にまたがるプログラム(if文など)を文字列として入れても実行することができます。しかし、今回は計算結果の返り値を利用するので、eval関数を利用します。
eval関数の使用例は次のようになります。
form = "89 * 97"
result = eval(form)
print(result)
#出力:8633計算機だけならばinputなどでこれを入力させて関数に代入などすればシェルだけで簡単に完結しますが、今回はボタンなどを本格的にtkinterで作っていくので、これは内部での利用になります。
classの利用
今回は関数間での変数の共有が多いので、関数をまとめることができるclassを使っていきます。classを使うと変数を$${\verb|self.変数名|}$$のように定義し、class内の関数の定義の最初の引数にselfを入れておくことで共有することができます。また、classの最初に$${\verb|__init__|}$$関数を入れるとclassが呼び出されると同時に実行され、classの初期設定ができます。具体的なコードの形は下のようになります。
class Test():
def __init__(self):
self.a = 2
self.b = True
def func_a(self):
print(self.a,self.b)
t = Test()
print(t.func_a)
#出力:2 Trueボタンと関数の紐づけ
今回はボタンが押されると指定した関数が実行されるようにします。しかし、関数には引数も指定しておきたいので、lambda文を使ってやっていきます。これは全体コードの項でご覧ください。
プログラムコード
長いように見えますが、細かく分けて考えれば単純です。
from tkinter import *
tk = Tk()
tk.title("Solver")
tk.resizable(width=False,height=False)
canvas = Canvas(tk,width=200,height=200)
canvas.pack()
class Solve():
###ボタン配置と変数の初期化
def __init__(self):
btn0 = Button(tk,text=" 0 ",command=lambda:self.n_app("0")).place(x=0,y=168)
btn1 = Button(tk,text=" 1 ",command=lambda:self.n_app("1")).place(x=0,y=142)
btn2 = Button(tk,text=" 2 ",command=lambda:self.n_app("2")).place(x=26,y=142)
btn3 = Button(tk,text=" 3 ",command=lambda:self.n_app("3")).place(x=52,y=142)
btn4 = Button(tk,text=" 4 ",command=lambda:self.n_app("4")).place(x=0,y=116)
btn5 = Button(tk,text=" 5 ",command=lambda:self.n_app("5")).place(x=26,y=116)
btn6 = Button(tk,text=" 6 ",command=lambda:self.n_app("6")).place(x=52,y=116)
btn7 = Button(tk,text=" 7 ",command=lambda:self.n_app("7")).place(x=0,y=90)
btn8 = Button(tk,text=" 8 ",command=lambda:self.n_app("8")).place(x=26,y=90)
btn9 = Button(tk,text=" 9 ",command=lambda:self.n_app("9")).place(x=52,y=90)
btndot = Button(tk,text=" . ",command=lambda:self.n_app(".")).place(x=26,y=168)
btnpm = Button(tk,text=" ± ").place(x=50,y=168)
btnreset = Button(tk,text=" C ",command=lambda:self.reset()).place(x=80,y=90)
btnplus = Button(tk,text=" + ",command=lambda:self.operator("+")).place(x=80,y=116)
btnminus = Button(tk,text=" - ",command=lambda:self.operator("-")).place(x=108,y=116)
btntimes = Button(tk,text=" × ",command=lambda:self.operator("*")).place(x=80,y=142)
btndiv = Button(tk,text=" ÷ ",command=lambda:self.operator("/")).place(x=106,y=142)
btnpow = Button(tk,text="^n",command=lambda:self.operator("**")).place(x=105,y=90)
btnequal = Button(tk,text=" = ",command=lambda:self.operator("=")).place(x=82,y=168)
self.a = '0'
self.b = '0'
self.ab = True
self.op = '+'
self.result = "None"
###画面のリセット
def reset(self):
canvas.delete('all')
self.a = '0'
self.b = '0'
self.ab = True
self.op = '+'
self.result = "None"
###数字の入力
def n_app(self,n):
canvas.delete('all')
if self.ab == True:
if self.a == '0' and n != '.':
self.a = n
else:
self.a += n
size = 20
if len(self.a) > 13:
size -= len(self.a) - 13
canvas.create_text(200,70,text=self.a,
font=('Consolas',size),anchor='e')
elif self.ab == False:
if self.b == '0' and n != '.':
self.b = n
else:
self.b += n
size = 20
if len(self.b) > 13:
size -= len(self.b) - 13
canvas.create_text(200,70,text=self.res+self.b,
font=('Consolas',size),anchor='e')
else:
self.reset()
self.a = n
size = 20
if len(self.a) > 13:
size -= len(self.a) - 13
canvas.create_text(200,70,text=self.a,
font=('Consolas',size),anchor='e')
###小数のいらない.0を削除(1.0 → 1, 0.250 → 0.25など)
def k(self,number):
if isinstance(number,float) and number.is_integer():
return int(number)
return number
###演算子の判定
def operator(self,operate):
if operate == "=":
self.result = self.a + self.op + self.b
try:
self.output(self.result)
self.a = str(self.k(eval(self.result)))
except:
self.output('Error')
self.a = '0'
self.b = '0'
self.ab = None
self.op = '+'
self.result = "None"
else:
self.op = operate
self.ab = False
self.b = '0'
canvas.delete('all')
self.res = self.a + operate
canvas.create_text(200,70,text=self.a+operate,
font=('Consolas',20),anchor='e')
###出力
def output(self,putdata):
if putdata == 'Error':
canvas.delete('all')
canvas.create_text(200,70,text='Error',fill="Red",
font=('Consolas',20),anchor='e')
else:
size = 20
if len(str(eval(putdata))) > 13:
size -= len(str(eval(putdata))) - 13
canvas.delete('all')
canvas.create_text(200,70,text=self.k(eval(putdata)),
font=('Consolas',size),anchor='e')
canvas.create_text(200,50,text=putdata,font=('Consolas',10),anchor='e')
solve = Solve()
tk.mainloop()
__init__関数の変数btnの列は一見複雑に見えますがウィンドウにボタンを作るプログラムなのでそこまで難しくはありません。
動作確認
最後に動作確認をします。上のプログラムを保存して実行すると、下のようなウィンドウが出てくるはずです。
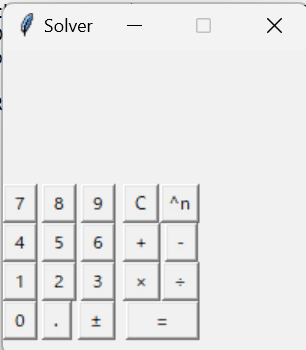
これで基本的な計算は完成ですが、まだ±の処理を追加していないのでこれは機能しません。このあたりと右の開いているスペースは次回の拡張編でやってきます。
それ以外の点は入力すれば基本的に動作すると思います。^nは$${x^n}$$という意味です。例として$${29^2}$$を計算してみます。

しっかり正しい計算結果が表示されました。
さて、今回はここまでです。次回はまだ製作中ですが、拡張編として三角関数やlogなども追加していきます!
