次の２つの結び目は同じ結び目ですか

　（きょうの算数・数学の記事は、小学１年生でも理解できるように書きたいと思います。でも小学１年生では読めない漢字や表現を使ってしまうと思いますので、おそらく読めるのは小学６年生以降のかたではないかと思います。「自分は算数や数学には縁がない」と思っておられるかたにも楽しくお読みいただけるように書きたいと思いますので、中高生・大学生・大学院生・社会人の皆さんも、よろしければぜひどうぞ。）

　（もうひとつ最初にお断りを。私の大学院での専門は２次元のトポロジーでした。以下に書く「結び目理論」は３次元のトポロジーです。つまり「低次元トポロジー」と言われる分野の、「お隣の次元」という関係にありました。たくさんの先輩・同輩・後輩が結び目理論を研究していまして、たくさんのセミナーを聞きました。ただしあくまで私とはちょっと専門が異なるものですから、あまり正確には書けないのです。じゃあこの記事は不正確か、というとそういうことはなく、正確に書きますので、そこはご安心ください。ただ、知らないことは「知りません」と明言して先に進むという書きかたをするということです。したがって、この記事は、結び目理論がご専門のかたがお読みになったら、はなはだ表面的知識で書いているなあ、と思われる可能性がありますので、そこだけ、お断りしました。つまり「難しいことを言わなければ、じゅうぶんに楽しめる」という記事を書きたいということです。）

　皆さん、つぎの２枚の絵を見てください。ひもがからまっています。こういうのを「結び目」というのですが（「結び目」の定義があいまいでごめんなさい。ひもが１本のとき「結び目」と言って、ひもが２本以上あるときを「絡み目」と言って区別するのですが、この記事には「結び目」しか出て来ません）、よく似ていますね。「いちばんできやすい結び目」だと言えると思います。片方を鏡で写したものが、もう片方になっていますね。こういうのを「三つ葉結び目（トレフォイル・ノット）」と言います。クローバー（三つ葉）みたいだからですね。

　さて、ここで問題です。この２つの結び目は、切ったり貼ったりしないで、片方から片方に移るでしょうか？つまり、この２つの結び目は、「同じ結び目」でしょうか、それとも「異なる結び目」でしょうか？

　これは、いきなり難しい問題に当たってしまいました。ごめんなさいね。じつは、この２つの結び目は、本質的に異なる結び目です。つまり、片方から片方へ、切ったり貼ったりしないで、互いに移りあうことができないのです。その理由は、少しあとに書きますね。（「理由」と言えるほどの理由は言えませんが。）

　では、以下の２つの絵を見てください。また、ひもがからまっていますね。こういうのは「８の字結び目」と言います。「８」という数字に形が似ているからですね。これも、片方を鏡で写すと、もう片方になります。

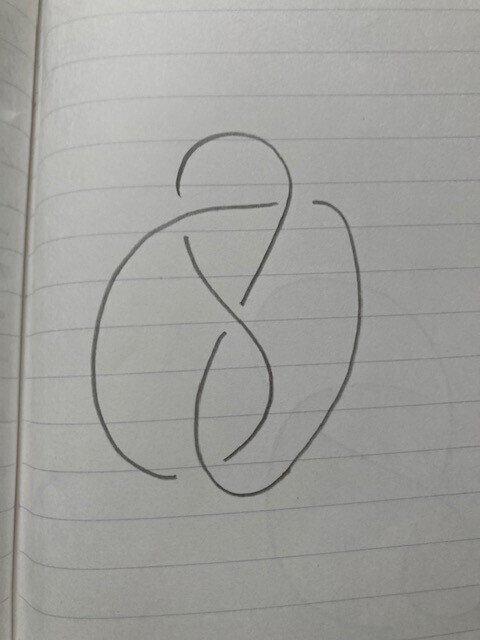
　さて、また同じような問題です。この２つの結び目は、片方から片方へ、切ったり貼ったりしないで、互いに移りあうでしょうか？これもすぐには答えられないことですから、答えを書いてしまいますね。

　これらは、移るのです！つまり、この２つの結び目は本質的に同じ結び目です！なんと！

　その理由は、小学生でも理解できるものです。「実際にやってみせる」というものだからです。以下の４枚の絵を見てください。ひもを動かしたり、全体を反時計回りに回したり、形を整えたりしていますが、ちゃんと、片方から片方へ移ることができたでしょう？

　このように、「２つの結び目は、切ったり貼ったりしないで、移りあわない」ということを言うのはたいへんです。おそらく結び目の「不変量」という概念を知らないと証明できないことではないかと思います（私も第一線を退いてから久しいですので、この16年間の結び目理論の進展を知らないで書いています。古い知識ですがおゆるしを）。でも「２つの結び目が同じである（連続的変形で移りあう）」ということは、小学生でもわかる証明があります。「実際にやってみせる」ということです。この話に、もう少しお付き合いください。

　私の手元にいま、落合豊行・山田修司・豊田英美子『コンピュータによる結び目理論入門』というちょっと（いやかなり）古い本と、村上順『結び目と量子群』というこれもちょっと（いやかなり）古い本が、計２冊あります。本日、私が参照する文献は、この２冊だけです。学生時代に買った本で、たまたま手元に残っている本です（学生時代の数学書は、あまりに要らなくて、多くはブックオフに売ってしまいました）。これ（落合・山田・豊田）に載っている例で、以下のような結び目があります。

　かなり複雑な結び目ですよね。じつはこれ、ほどけるのです！つまり、これは以下の図のような「輪ゴム状態」の結び目（結んでいないのに「結び目」と言うことをおゆるしください。「ゼロ」を「数」というようなものだと思ってください。こういうのを「自明な結び目」と言います）に、切ったり貼ったりしないで、連続的に移るのです！つまり、「ほどける」のです。こういうのを、どうやって証明したらいいですか？これ、「実際にやってみせる」しかないのですよ！

　もうひとつ、同じ本に載っているすごい例を挙げますね。つぎの２つの結び目です。

　違う結び目に見えますよね。実際、（以下はその本の受け売りです）19世紀の終わりごろ、リトルという数学者が結び目の分類をしたとき、この２つの結び目は、異なる結び目であると分類されたそうです。ところが、それから約80年後の、1974年に、（それでも現在から見たら半世紀くらい前の話ですが、）パーコという数学者が、じつはこの点においてはリトルの分類が間違っていて、この２つの結び目は同じものであることを証明しました。その証明もこの本に載っていますが、連続的な変形の途中経過の絵をぜんぶで７枚描いて、「小学生でも理解できる」ような証明をしています。しかし、これ、気の遠くなるような話ではないですか？80年かかったとしてもふしぎではないくらい、極めてたいへんなことです。

　では、最初に挙げた２つの「三つ葉結び目」が「移りあわない」「本質的に異なる」結び目であることは、どうやって言ったらいいのでしょう。「いろいろがんばってみましたが、うまくいきませんでした。ダメです。移りあいません」というのは証明になっていません。「きみのがんばりかたが足りないからだ」と言われたら、返す言葉がないでしょう？そこで、さっきちょっと言葉を出しましたが「（位相）不変量」というものを使うのです。

　「位相不変量」とは「同じ形だったら同じ値を返す」というものです。位相不変量で、高校生でも知っているものがひとつあります（以下は高校生以上の人向けの記述になります）。多面体の「（頂点の数）－（辺の数）＋（面の数）」は、必ず「２」になったことを覚えておられるでしょうか。これはオイラー数（オイラー標数）といい、たとえばこれを「ドーナツの表面」でやると、この数は「２」ではなく「０」になりますよ。（いつかオイラー数でも記事を書きたいですね。）高校生以上向けの記述はここまでで終わりです。

　さて、「同じ形だったら同じ値を返す」ということは「違う値を返したら違う形だ」ということが言えます。（高校生なら「対偶」という言葉を知っていますよね。また高校生以上向けの記述おしまい。）以下は、あるセミナーである先生が言っていたたとえです。あまりにうまいたとえなので、覚えています。借りますね。「血液型が違ったら違う人だとわかる」。その通りですね。そして、血液型が同じだったら同じ人だとはぜんぜん言えませんよね！というわけで、位相不変量が同じだったら「同じ」だとはぜんぜん言えないのですが、位相不変量が違ったら「違う形だ」と言える、というわけです。最初に挙げた２つの三つ葉結び目は、少なくとも「ジョーンズ多項式」と言われる結び目の不変量が異なります。（「多項式」という言葉を習うのがまた高校時代ではないかと思いますが、そんな、ジョーンズ多項式に深入りするつもりはありませんので、知らなくてもだいじょうぶです）。ここで２冊目の村上順先生の本を参照します。三つ葉結び目のジョーンズ多項式は、片方が$${-t^4+t^3+t}$$で、もう片方が$${-t^4-t^3-t}$$です。（普通どちらのがどちらなのかよく知らないのですが、おそらく私が描いた順番であっているだろうと思います。）とにかく、２つの三つ葉結び目で、違う多項式が出て来たことがわかります。これで、２つの三つ葉結び目が移りあわないことの証明は終わりです！

　以下はまたちょっと難しい話（というか私が詳しいとは言えない話）になってしまうのかもしれませんが、ジョーンズ多項式というのは、もともと作用素環という分野の研究者であるジョーンズによって定義されたものであり、ただし、トポロジーの人は、このジョーンズ多項式なども、トポロジー的に計算します。さっきからお見せしている、結び目をこうして２次元の紙で見ている絵を「ダイアグラム」と言いますが、ダイアグラムから不変量を定義するのです。そして、それが結び目の不変量であることを言うには、以下のようにします。以下の３枚の絵は「ライデマイスター・ムーヴ」と言います。結び目の一部分を描いた、結び目を変形する絵ですね。３種いずれの変形においても、結び目が変わらないことはすぐにお分かりいただけると思います。

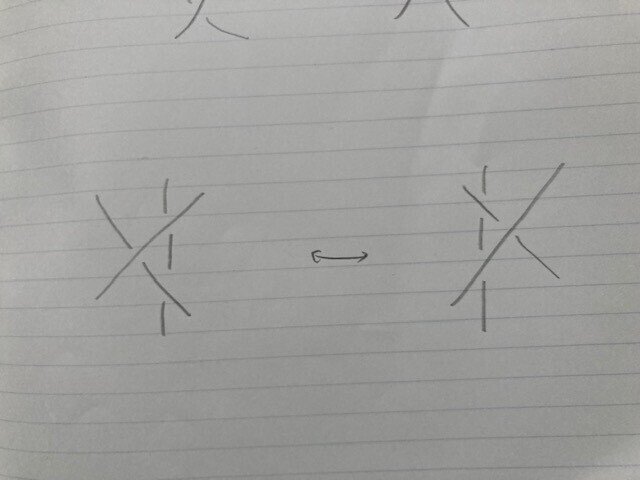
　しかし、ライデマイスター・ムーヴのすごいところは「同じ結び目だったら、すべてこの変形だけで移りあう」ということが言えていることです！（このことは誰が証明したのか、またどうやって証明するのかは、私は知らないことです。名前からしてライデマイスターさんという人が証明したのかな。）だから、ダイアグラムから定義した結び目の不変量が、ほんとうに不変量になっていることを言うのは、ライデマイスター・ムーヴで変わらないことを言えばよいわけです。以上、私が院生のころ「お隣の次元の分野」のお話として、よく聞いた話をまとめました。専門家ではないので、きちんと書けなくてごめんなさい。なるべくウソを書かないように気を付けて書いています。

　とにかく、「２つの結び目は異なる（移りあわない）」ことを言うのは、ときどきすごくやさしい場合があります。「不変量が異なる」ことを言うだけですんだりするからです（結び目理論をなめた言いかたに聞こえましたらすみません）。でも、「２つの結び目は同じである（移りあう）」ことを言うのは、とてもたいへんだったりします。さきほどの「パーコの80年ごしの証明」みたいに、実際にやってみせなければいけないからです。小学生でも理解できる証明は、後者ですけどね。（「血液型が同じでも同じ人とは言えない」「生年月日が一致しても同じ人とは言えない」という感じで、不変量がいくら一致しても同じ結び目だとは言えませんので。）

　（もうひとつ、結び目理論がなぜ「３次元の」トポロジーと言われるのかを少しだけ書いておきますね。結び目って、４次元の世界に行ったら、すべてほどけてしまうのですよ！だから結び目とか絡み目というのはあくまで３次元の世界での話です。同様に、４次元のなかでの２次元の多様体（曲面）の「結び目現象」を研究しているかたのセミナー発表も聞いたことはありますが、それはここまで述べてきたことに比べるとかなりマイナーな研究になります。）

　どうも「小学１年生でも理解できる」と宣言して書き始めたわりには、（余談と称してですけど）だいぶ難しい話も出て来てしまいました。でも、言いたかったことは、「三つ葉結び目は鏡に写したら異なる結び目になってしまう」ことと「８の字結び目は鏡に写しても同じ結び目である。その理由を述べるには実際にやってみせるしかない」ということくらいですので、小学１年生でも理解できると宣言して書き始めたのです。少し思うのは、これって大学院の専門数学なのですけど、こういうのって、大人が考えるより、子どもで、すごい直観を働かせる人がいるのじゃないのかな？ということです。あるいは、サヴァン症候群とか共感覚の人で「この結び目とこの結び目は違う」とか「この結び目とこの結び目は同じ」って、瞬時に判定できる人はいるのではないの？ということもちょっと思うわけです。

　いかがでしたでしょうか。ほんとうにおもしろい話だったかどうかはあまり自信がありませんが、私が大学院のときの「すぐお隣の専門分野」としてしばしば話を聞いてきた話を少しだけご紹介いたしました。でも、きっと、ちょっとだけおもしろいでしょう？ちょっとでもおもしろかったら、どうぞ「スキ」押してくださいね！本日の算数・数学のお話は以上です！