ポール・ディラックの原論文を読んでみよう（1926年：q 数の登場）

今回取り上げるポールくんの論文は "Relativity Quantum Mechanics with an Application to Compton Scattering"（相対論的量子力学に向けて：コンプトン散乱への応用）。1926年4月29日受理。

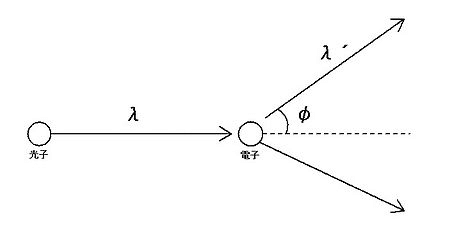
コンプトン散乱というのは… 光子を電子に当てると、電子が跳ねとんで、それから光子の波長が変わる現象です。高校物理の終盤「原子物理」でちらっと出てきます。

光は波だとずっといわれてきたのを、アインシュタインが「波であるが粒子でもある」とする「光量子」説を1905年に提唱しました。これには元ネタがあって、５年遡って1900年にプランクが提唱した「光のエネルギーは整数倍つまりデジタルである」とする説が始まりでした。プランクそのひとは「たぶん物質の内部構造の関係で整数倍になるのだろう」と考えたのを、若きアルベルトくんは「気体分子の数式となんだか似てしているし、光も粒子と考えていいじゃないでしょうか」と言い出して、発表当時はAHO扱いされたのでした。

しかし１１年後の1916年、ミリカンがミツカン…ではなくて油滴を使った巧妙な実験装置によって電子の電荷量の正確な測定に成功し、アルベルトくんの計算値と合うことを示したことで、学界でＡＨＯ扱いされた彼の光量子説が息を吹き返したのです。アインシュタインといえば相対論の偉い学者というイメージがあるのですが、相対論が比較的短期間で定説として受け入れられたのに対し、光量子説は「あいつ頭おかしい」と言われ続けた苦難の子で、しかしミツカン…ではなくてミリカンの油滴実験によってアルくんの説に基づく計算値によく合う値が出たことで、学界の趨勢が一気に変わったのです。この大逆転劇に敬意を表してか、ノーベル賞委員会は彼への物理学賞授与にあたっては相対論ではなく光量子説の功績を称えたほどです。1921年のことです。

翌1922年、アーサー・コンプトンが、Ⅹ線つまり極めて波長の短い光を、モリブデン（下の絵で「石墨片」とあるもの）にあてて、反射したものをスリットや単結晶を経て、電離箱で測定するという実験を行って、アインシュタインの光量子説を裏付けるばかりかより具体的な測定値を出しました。

冒頭でお見せしたこれです。Ⅹ線（つまり光子）を電子にぶつけると、ぶつかる前と後とで波長が違ってくることを示したわけです。

今回取り上げるポール・ディラックの論文（1926年）は、これを彼独自の数学的技法によって説明に挑む内容です。ちなみに博士論文を仕上げるより数か月前に書き上げていますね。

ブツを見ていきましょう。全12頁の、冒頭から。

The new quantum mechanics, introduced by Heisenberg and since developed from different points of view by various authors, takes its simplest form if one assumes merely that the dynamical variables are numbers of a special type (called q-numbers to distinguish them from ordinary or c-numbers) that obey all the ordinary algebraic laws except the commutative law of multiplication, and satisfy instead of this the relations

[ここに数式①]

where the p's and ^’s are a set of canonical variables and h is a c-number equal to (2tc)- 1 times the usual Planck’s constant. Equations (1) may be regarded as replacing the commutative law of the classical theory, as one can, with their help, build up a complete algebraic theory of quantities that are analytic functions of a set of canonical variables. Further, it may easily be seen that the quantity \x, y\ defined by

[ここに数式②]

is completely analogous to the Poisson bracket of the classical theory. By means of this analogy the whole of the classical dynamical theory, in so far as it can be expressed in terms of P.B .’s instead of differential coefficients, may be taken over immediately into the quantum theory.

DeepL さん日本語にしてくださる？　「うんいいよ」：

ハイゼンベルクによって導入され、その後さまざまな著者によって異なる観点から発展してきた新しい量子力学は、単に動的変数が特殊なタイプの数（通常の数またはc数と区別するためにq数と呼ばれる）であり、乗法の可換則を除く通常の代数法則すべてに従うと仮定すると、最も単純な形になる。

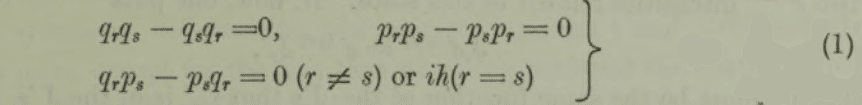
ここでpと^は正準変数の集合であり、hは通常のプランク定数の(2tc)-1倍に等しいc数である。式(1)は、古典理論の可換則に取って代わるものと見なすことができる。なぜなら、その助けを借りて、カノニカル変数の集合の解析関数である量の完全な代数理論を構築することができるからである。によって定義される量 ⊖x, y は、ポアソン関数に完全に類似している。

で定義される量は、古典理論のポアソン括弧に完全に類似している。この類推によって、古典力学理論の全体は、微分係数の代わりにポアソン括弧で表現できる限りにおいて、量子論に直ちに引き継ぐことが可能ではないかと思われる。

ポアソン括弧については、この論文より一年前、彼はこんな主張をしています。前に当ブログで取り上げた論文です。こんなのです。

ハミルトン力学つまり現代でいう力学的エネルギー保存則に軸足を置いた力学で使われる、特別な括弧です。ハミ力学は量子力学より前の時代に形になったものですが、同力学におけるこの括弧は、その後の量子力学で頻繁に表れる式「ＡＢーＢＡ≠０」と同じ形をしていますね。これに着目すれば、旧来の力学を量子論に拡張できると、ポールくんはかっこよく宣言しているのです。

ｑ数についてはここの終盤で説明したとおりです。アイディアは前年に提唱していて、ｑ数と命名したのがこの論文から…だと思います。後日もう少し前の論文もチェックしないと断定しかねますがたぶん今回取り上げているこの論文冒頭からと思われます。［追記：この論文よりさらに三か月前に投稿した論文のなかでｑ数とｃ数についてディラックが解説しているのを見つけました。詳細はこちら］

論文の続きを見ていきましょう。

It now remains only to determine what values one shall assume the k s to take, and this may require an appeal to physical considerations. For the case of the simple harmonic oscillator it has been shown rigorously by Born and Jordan that the action variable can take only a certain discrete set of values, one of which gives a state of lowest energy, and their method seems to be capable of extension. For the case of Compton scattering by a free electron, considered in the present paper, there is no restriction on the values that the action variable can take. The initial value of the action variable is now determined by the initial velocity of the electron, which must, of course, be given from physical considerations.

DeepL さん訳してちょ。「うんいいよ」

あとはk sがどのような値を取るかを決めるだけであるが、これには物理的な考察が必要であろう。単純な調和振動子の場合、ボルンとヨルダンによって、作用変数はある離散的な値の集合しか取り得ないこと、そのうちの1つはエネルギーが最も低い状態を与えることが厳密に示されている。そして彼らの方法は拡張可能であるように思われる。本論文で扱う自由電子によるコンプトン散乱の場合、作用変数が取り得る値には制限がない。作用変数の初期値は電子の初速度によって決まるが、これはもちろん物理的な考察から与えられなければならない。

ボルンとヨルダンによってどうのこうのとあるのは、前年（1925年）にこの二人組がひねり出したこの数式のことです。

ＰＸーＸＰ＝ (h/2πí)Ｉ

前に触れた覚えがありますこれについて。ＰとＸはそれぞれ行列です。ディラックは当時この論文のことを知らなくて、上述のポアソン括弧のアイディアをもとに同じ形式の（しかしもっと洗練された）数式を導出していました。その論文をハイゼンベルクに送ったところ「ボルンとヨルダンが二か月前に同じ数式を論文にしている」と返信があってポールくんびっくりという、あの論文です。

今回論じている論文のなかでディラックは、この数式に触れつつ、コンプトン散乱についてはぼくのやり方でスマートに説明してみせるぜっと述べているわけです。

結論を先にいうと、少しばかり早すぎました。特殊相対論に対応した理論の確立には、もう２年かかりました。

それでもかなりの精度です。「Classical Theory」つまり旧理論ではこうなるという破線は、ⅹがⅹⅹⅹと続く、つまり実験による測定値の並びから大きくかけ離れています。下の方に「Compton's Theory」（コンプトンによる理論から導出される値）の破線グラフがあって、これはかなりよくⅹⅹⅹに寄り添っています。ディラックによる理論（「New Quantum Theory」）のものも、コンプトンの理論のものと同じくらいには観測値によく寄り添っていますね。

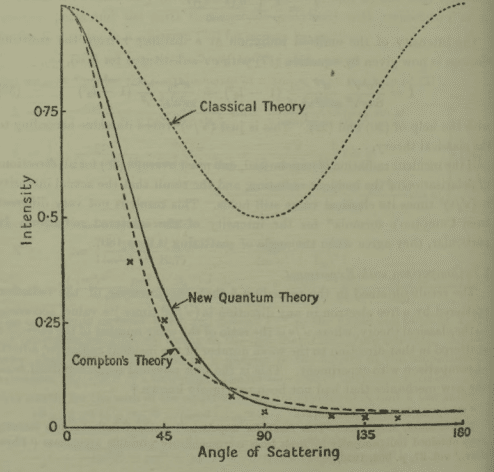
この表を見せつけつつポールくんはこんな風にこの論文を締めくくります。

According to the present theory the state of polarisation of the scattered radiation is the same as on the classical theory, since the intensity of either polarised component of the scattered radiation in any direction is (v'/v)3 times its classical value. The radiation scattered through 90° is thus plane polarised for unpolarised incident radiation. This result might have been expected from the correspondence principle, since it holds on the classical theory for an electron moving with either the initial velocity (i.e., zero) or the final velocity of the quantum process. I t does not hold for an electron recoiling with th a t velocity that gives the correct frequency distribution when the electron is scattering according to the classical theory, and for this reason previous theories have predicted a shift from 90° for the angle of scattering which gives plane polarisation. J Experiments have been performed by Jauncey and Stauss to settle this question.§ They found no shift with incident radiation of 0*54 A, and a shift of 2^°, less than half the value they expected, with incident radiation of 0 -25 A, these results are slightly in favour of the present theory which requires no shift. Great accuracy was not attainable owing to the difficulties caused by stray radiation.

DeepL さん訳してちょ。「うんいいよ」

私の理論によれば、散乱放射線の偏光状態は古典的理論と同じであり、散乱放射線のいずれかの方向の偏光成分の強度は、古典的値の(v'/v)3倍である。このように、90°方向に散乱された放射線は、偏光していない入射放射線に対して平面偏光している。この結果は、対応原理から予想されたことかもしれない。なぜなら、対応原理は、量子過程の初速度（つまりゼロ）または終速度のいずれかで運動する電子に対して、古典理論で成り立つからである。しかし、電子が古典的理論に従って散乱するときに正しい周波数分布を与えるような速度で反跳する電子に対しては、対応原理は成り立たない。この問題に決着をつけるため、JaunceyとStaussによって実験が行われた§。彼らは、0*54 Aの入射放射線ではシフトがなく、0 -25 Aの入射放射線では2^°のシフトと、彼らが予想した値の半分以下であることを発見した。この結果は、シフトを必要としない私の理論にわずかに有利である。

「わずかに有利」（slightly in favour）で締めくくっていますが、要するに完全ではないってことです。光子を電子にぶつけるわけだから、特殊相対性理論準拠の理論でないと完全にはなりえないことを、ポールくんもわきまえていたのでしょう。

彼の方針は一貫しています。「特殊相対論にも沿うような量子力学を作り上げるという悲願を果たすためには、ポアソン括弧準拠に整えるのが先決であり、そのためにはｑ数の導入が欠かせない。その実例をコンプトン効果の説明でお見せする。相対論には対応していないがかなりいいところまで観測値に迫っているではないか。ｑ数化 → 特殊相対論化 の方向性で、行けるぜっ！」

この野望を、彼はわずか２年後にやってのけることになります。