ペンローズ・タイルやアインシュタイン・タイルについて書かれた『ペンローズの幾何学』を購入したので、書いてみる。
前回は雑談でした。
本来ならば、前回書くべきでした話を、今回書きます。
やっと出たなあ
ということで、こちらの本です。
『ペンローズの幾何学』でございます。
【内容紹介の引用】
ペンローズが追い求めた「驚きの図形」が見つかった!
世界中の数学ファンを熱狂させたペンローズ・タイルの発表(1974年)から半世紀──。
「隙間も重なりもなく平面を敷き詰める図形」=平面充填を探究するシンプルな問題は、幾何学を発展させ、結晶科学においてはノーベル賞をもたらす成果を挙げてきた。
2023年には、「存在しない」と考えられてきた図形「アインシュタイン・タイル」がついに発見された。
非周期モノ・タイルとよばれるこの図形は、いったいどんな形状で、どこがどうすごいのか?
数学者だけでなく、アマチュア愛好家によっても偉大な発見が続々となされてきた平面幾何の世界。
パズル感覚で楽しむことができ、しかも奥行きの深いこの分野で、「次の大発見」をもたらすのは、あなたかもしれない!
ということです。
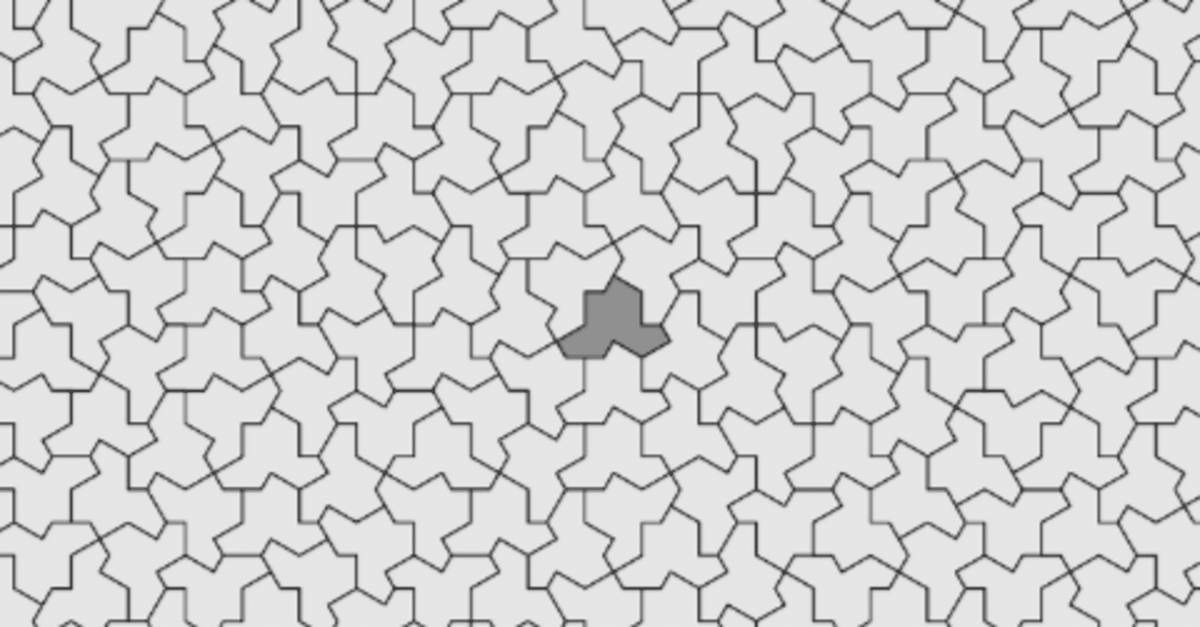
アインシュタイン・タイルとは
例えば、これです。

なんか凸凹した図形です。
この図形ですが、平面に隙間なく敷きつめることができます。

敷き詰めることができるのですが、周期的なパターンがありません。
周期的パターンのない敷き詰めができる図形で、有名なのはペンローズ・タイルです。
ペンローズ・タイルは2種類の図形を組み合わせています。
ノーベル物理学賞受賞者のロジャー・ペンローズが1970年代に提唱した図形です。
2種類でできることがわかったので、
ほなら、1種類のみでできるヤツあるんか?
となります。
この図形を見つける問題を、ドイツ語の「1(ein)」と「石(stein)」を組み合わせて「アインシュタイン問題(einstein problem)」と名付けました。
結局、50年以上かかっても見つからなかったヤツが、去年(2023年)ヒョコッと発見されたのでギャーっとなったわけです。
その図形が、先にお見せした凸凹のやつで

スミスの帽子(Smith HAT)とも呼ばれます。
スミスとは、この図形の発見者John Smith(ジョン・スミス)さんを指し、スミスさんは数学者ではなく元タイル職人の数学愛好家(つまり、数学アマチュア)です。
正直、遊びすぎてます
『ペンローズの幾何学』を紹介しましたが、アインシュタイン・タイルについて結構な分量で書かれた書籍はほとんどありません。
発見されてまだ1年しかたっていないこともあります。
とはいえ、スミスさんの発見したタイルは非常にいじりがいのあるネタでして、去年の4月からちょいちょいこのタイルにまつわる記事を好き勝手に書かせていただきました。
えーっと、どんだけ書いたかな……20本書いてました。
個人的に書いて面白かった記事をいくつかピックアップすると、
発見されたアインシュタイン・タイルを2つの点対称図形に分割してみる試み。
やりすぎて「虚数面積の図形」という訳わからん概念まで引っ張り出してきました。
アインシュタイン・タイルの中でも特定の図形(仮にTile(1,1)と呼ぶ)が、カイロ五角形と正三角形を組み合わせて作ることができる話。
Xを通じて妙な感じで広がってびっくりした。
そのTile(1,1)。
2つの点対称図形に分割した2種類の図形が、実は異なる非周期敷き詰めパターン「Wheel Tiling」だったと知り、びっくりした。
びっくりしっぱなし。
締め
ということで『ペンローズの幾何学』の紹介(なのか?)でした。
著者は谷岡一郎さん、荒木義明さんです。
荒木さんには、Xのコメントなどからたくさんの情報やコメントから、記事を書くモチベーションをいただきました。
ありがとうございます。
次回はどうしましょうかね。
では。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
