
確率の基礎の基礎についてのなるべく分かりやすい解説
確率については色々な話があるのですが、「そもそも確率とは何か」というとことを考えてみると、物事の起こりやすさを数値的に表したものということになります。それ以上でもそれ以下でもありません。
しかし、そうなると次の問題は「物事の起こりやすさはどうやって数字で表現したらいいのか」ということになります。ここで認識しておかなければならないのは、確率はあくまで人間が勝手に作り出したもの、という点です。確率の計算方法は宇宙の法則で決まっているのではなく、人間が能動的に「こうやって確率を計算しよう」と決めるわけです。
そうすると、確率の計算方法は十人十色、無数にあって良いということになります。確かにそれはそうなのですが、その中でも、人々に広く受け入れられているものがあります。それがどんな計算方法かというと、端的に言ってしまえば、「合理的」なものです。今の段階ではまだピンと来ないかもしれませんが、これから具体的に計算方法を見てゆく中で、この点については明らかになると思います。
確率では大抵コイン投げの例が出てきますが、この解説でも使うことにしましょう。
コインを投げるという行為を考えた時、「表が出る」という物事の起こりやすさを、どうやって数字で表したら良いか、という問題を考えるわけです。今、コイン投げの結果には二通りあると考えられます、それは「表が出る」と「裏が出る」というものです。
……と、普通の解説なら始めるでしょうが、しかし、本当にそうでしょうか? コインを投げた結果、たまたまコインが立つということもあり得るでしょう。また、使っているコインがばらばらになるということもあり得るでしょう。というか、コインを投げて起こりうる結果には、無数の可能性があります。(コインを猫が咥えてどっかに行くとか、地球が爆発するとか。)
そこで、(確かに実際はコイン投げの結果には無数の可能性があるのですが)今考えている「コイン投げ」という行為には「表が出る」と「裏が出る」という2つの結果しか起こらないと「仮定」しましょう。物理学でも、例えば力学では、摩擦を無視した理想状態を考えるということがありますが、今の「コイン投げ」はそういう理想的、あるいは仮想的なコイン投げを考えているわけです。どうしてこんな理想的な状態を考えるのかというと、摩擦を無視することも同じ動機なのですが、そういう理想化された状況のほうが、問題の本質が見えてくるからです。そうしてまず、非常に簡単な状況で問題を解いてみて、より複雑な状況にそれを応用してゆくというのが、科学者がよく使う方法になります。コインが立ったりすることまで考えるのは、理想的なコイン投げで確率の本質を見てからでも十分です。
さて、今、理想的なコイン投げにおいては「表が出る」か「裏が出る」の2通りの可能性しかありません。「表が出る」という物事の起こりやすさはどうやって計算すれば良いでしょうか。最初に述べたように、色々な計算方法があり得ますが、現在一般に広く受け入れられている方法は、次のようなものです。
まず、「表が出る」と「裏が出る」には「チャンス」を割り振ると考えます。より多くチャンスが割り振られた方が、より起こる可能性が高くなるとします。また、割り振れるチャンスの総量は1としましょう。(100でも良いですが、その場合は起こりやすさがいわゆる「パーセント」で計算されることになります。)視覚的に分かりやすくするなら、次の図のようになります:

これをどうやって「表が出る」と「裏が出る」に割り振るかということですが、2つに優劣が無いのであれば、その割り振り方は次の図のようにするのが合理的でしょう:
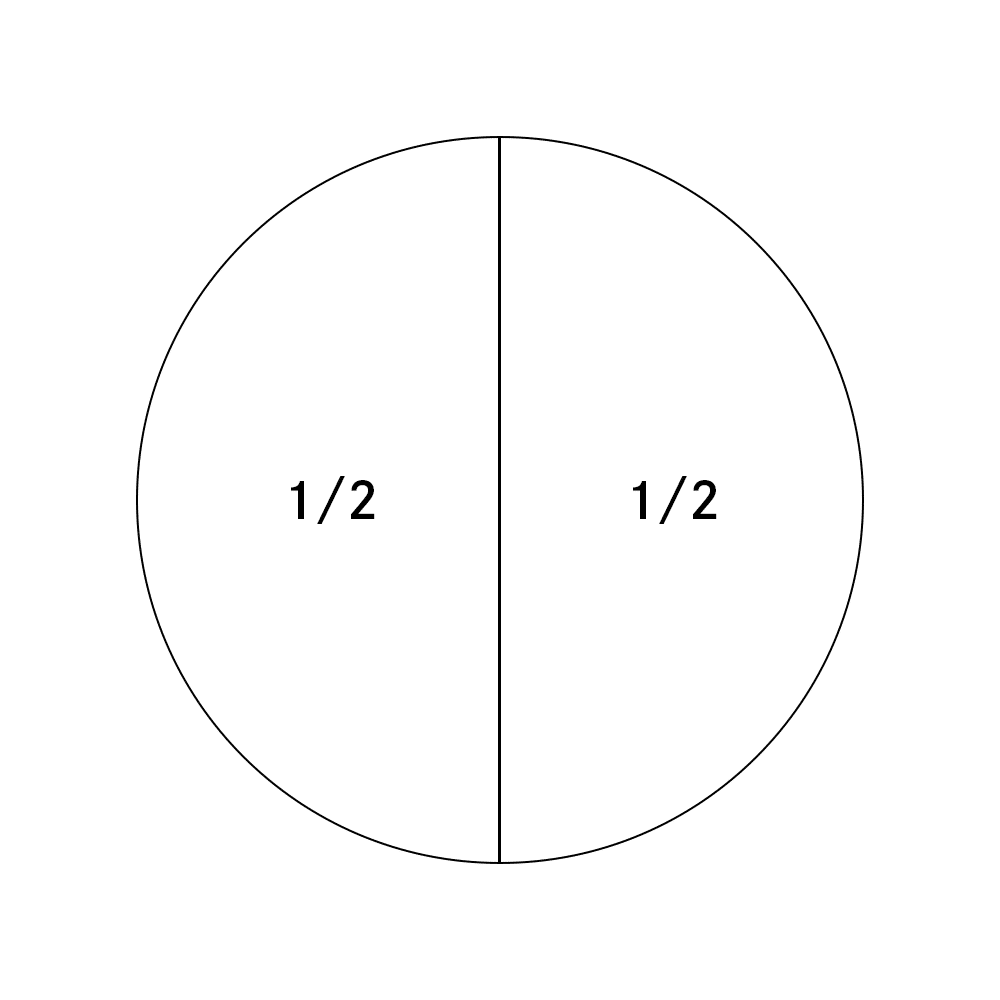
要するに半分に分けるということです。総量が1なので、半分に分けるとそれぞれ1/2ということになります。そしてこの割り振られたチャンスの量を、その物事が起きる確率とします。なので「表が出る」という物事が起きる確率は1/2ということになります。もちろん、「裏が出る」も同様に確率が1/2となっています。この確率の計算方法は合理的でしょうか? 少なくとも直感的には正しいような気がしないでしょうか。そんなわけで、この計算方法が広く用いられているわけです。
さて、こうしてコイン投げについて確率を計算することが出来ました。振り返ってみると、この方法で本質的な重要性を持つのは「確率を計算したい物事について、チャンスをどれだけ割り振るか」ということ、その方法に尽きます。なぜなら、その割り振られたチャンスの量がそのまま確率になるからです。上で見たコイン投げの場合、「表が出る」と「裏が出る」という物事に「優劣がない」から、それぞれ同量のチャンスが割り振られなければならないと考えた結果、1/2ということになりました。そして実のところ、この「優劣がない物事には同量のチャンスを割り振る」ということが、これからこの方法で確率を計算してゆく上で使う唯一の原理になります。
では物事に「優劣がない」ということは、この場合、どういうことでしょうか。それは「起こりやすさに違いがない」ということです。なるほど確かに、コイン投げについて「表が出る」と「裏が出る」の2つの結果の間に「起こりやすさの違いがない」のは明らかに思えます。
……しかし、ちょっと待って下さい。ここで私たちは重大な局面を迎えています。私たちは「表が出る」ことの確率、つまり起こりやすさを計算することを目指してここまでやってきました。しかし、その計算の過程で「表が出る」ことと「裏が出る」ことの起こりやすさが同じであるという仮定を使いました。起こりやすさを計算する前に、どうしてこの2つの物事の起こりやすさが同じだと分かるのでしょうか? 計算して初めて2つの物事の起こりやすさが同じであると分かるのではないでしょうか。
こういうように、「鶏が先か、卵が先か」という話になってしまった場合、非常に有効な考え方があります。それは「結果だけ見る」というものです。今の場合、上で述べた確率の計算方法によって、どのように確率が計算されるかという結果だけを見てみます。
1.起こり方に「優劣がない」物事をすべて列挙する。
(コイン投げの場合は「表が出る」と「裏が出る」の2通り。)
2.列挙した物事の数がN個であった場合、それぞれの確率を1/Nとする。(コイン投げの場合はそれぞれ1/2となる。)
問題は、1番です。確率を計算する前にどうして優劣がないかどうか分かるのかということです。では、コインの場合、どうして「表が出る」と「裏が出る」の2つの物事の間に優劣がないと分かったのでしょうか。
実はここが問題で、何も「分かって」などいないのです。なぜなら、この優劣の有無というのは、あくまで仮定、仮説に過ぎないからです。実際、今のコイン投げの例では優劣が無いと仮定しましたが、本当は優劣があると考えるのが自然です。なぜなら現実世界にあるコインは100%精密な作り方はされていませんから、どうやっても表と裏に歪みがあるはずだからです。ですから、もし精密な実験を行えばコインの表と裏について、どちらかが出やすいという結論になると考えるのが妥当です。優劣が無いというのは、100%精密なコインを想定しているようなもので、そんなものはこの世界に存在しないでしょう。しかしそれでも、物理的世界を理想化した極限では、100%精密なコインというものを想像することは出来ます。そして途中でも述べたように、そういう理想的な状況というのは、理論を構築する上でのモデルケースとなるため有用なのです。
つまり、結論としては、コインの「表が出る」と「裏が出る」に優劣がないというのは計算を行う上での仮定に過ぎないということです。
ところで、純粋に論理的に言えば、仮定はどんなものを採用しても良いのですが、確率を現実世界に応用したいと考える時には、仮定の妥当性という問題は残ります。あまりに現実離れした仮定を設けてしまえば、そこから出てくる結論も、現実離れしてしまうでしょう。それでは確率を現実世界に応用したいという目標が達成されません。しかし今の場合、コインが100%精密だと仮定することは、そこまで現実離れした仮定ではないと思われます。もちろん、最終的には、確率を計算しようとしているシチュエーションに依って、仮定がもっともらしいか否かを決めるのです。
そうして、兎にも角にも一度優劣のない物事を設定してしまえば、後はそれらにチャンスが割り振られ、確率が決定されることになります。どんな物事を優劣なしに設定するかは、本来計算する人間の自由ですが、もしそれを物理現象に応用することが目標であれば、設定の仕方はある程度妥当性を持たせる必要がある、ということになります。
以上が、確率の基礎の基礎についての話です。
最後に、数学の「同様に確からしい」という用語について見ておきます。
今までの解説では「優劣がない」と表現していたものは、数学の専門用語では「同様に確からしい」と呼ぶだけの話ですが、この日本語は、今までしてきた議論を踏まえると、よく出来たものだと感心します。「同様に確か」というのは、「起こり方に差がない」ことを表しており、最後の「~らしい」というのは、それがあくまで仮定であることを推量の形で表現しています。実際、コインの表裏が同様に確からしいと言った時に「それは本当ですか?」と聞かれると、それを証明することは出来ず、本当のところは分からないのです。私達に出来るのは、精一杯妥当な仮説を立て、最後のところでは「それはあくまで計算をするための仮説です」と逃げることだけです。「本当のところ」は誰にも分からないので、それで良いのです。もし、それでも「その仮説はおかしい」という話になったら、「この仮説をどうしても受け入れられないなら、これ以上議論は出来ませんね」と言うだけです。同じルールが共有できる人たちだけで、議論をすれば良いのです。
ただ、お互いに分かり会えるチャンスはあります。その仮説そのものではなく、その仮説をおいて出てくる結果がどれだけ正しいかを見るのです。仮説の正しさそのものはなかなか検証出来なくとも、結果については実験によって正しいかどうかを検証することが出来るからです。
もちろんそれでも、妥当性が高まるだけで「本当に」正しいかどうかはどうやっても知ることは出来ません。なので、非常に冷めた見方をすれば、「こういう仮説をおけば、こういう結果が出てきます」とだけ言うのが一番安全であり、実際、現代数学はこの立場を採用しています。「それが本当に正しいか」という価値判断は行わないことにしているのです。もっと言えば、この立場を極限まで精密化した「公理主義」に基づいて全ての数学理論を作り上げています。この辺りの事情についてはまた別の記事で解説できればなと思います。
次回はサイコロ投げのような少し複雑な例について考えることにします。
この記事が気に入ったらサポートをしてみませんか?
