
【自由研究】ペットボトルキャップで数学してみた(ピタゴラス数)【前編】
3と4と5
この3つの数の組み合わせを見て、「あ~、あれね!」と思い浮かんだ方は数学脳です(笑)
この記事では、この「3,4,5」のような3つの数はどんな数なのかを紹介し、同じ性質をもった3つの数の組の見つけ方をペットボトルキャップを使って見つけていきます。
また、今回の内容は、【前編】【後編】の2編構成にしました。
理由は、長いからです。(笑)
もっと簡潔に書ければいいのでしょうが、語彙力無くてすみません。
最後まで読んでいただけるとうれしいです。
1 3,4,5はどんな性質をもってる?
3,4,5という数字は、こんな性質があります。
$${3^2+4^2=5^2}$$・・・①
このような性質をもっていて、このような3つの数の組み合わせをピタゴラス数といいます。
{3,4,5}が①の式を満たすなら、それぞれを2倍や3倍した{6,8,10}や{9,12,15}もピタゴラス数です。
また、{6,8,10}や{9,12,15}は、3つの数を2や3で割り切ることができるのに対して、{3,4,5}は1でしか割り切れません。このように、3つの数を1でしか割り切れない場合のピタゴラス数を原始ピタゴラス数といいます。
わかりやすく下の図にまとめました。また図のような疑問が生まれました。

「ピタゴラス」と聞くと、中学校で学習したピタゴラスの定理を思い出すと思います。

先ほどの3,4,5の3つの数の組み合わせであれば、
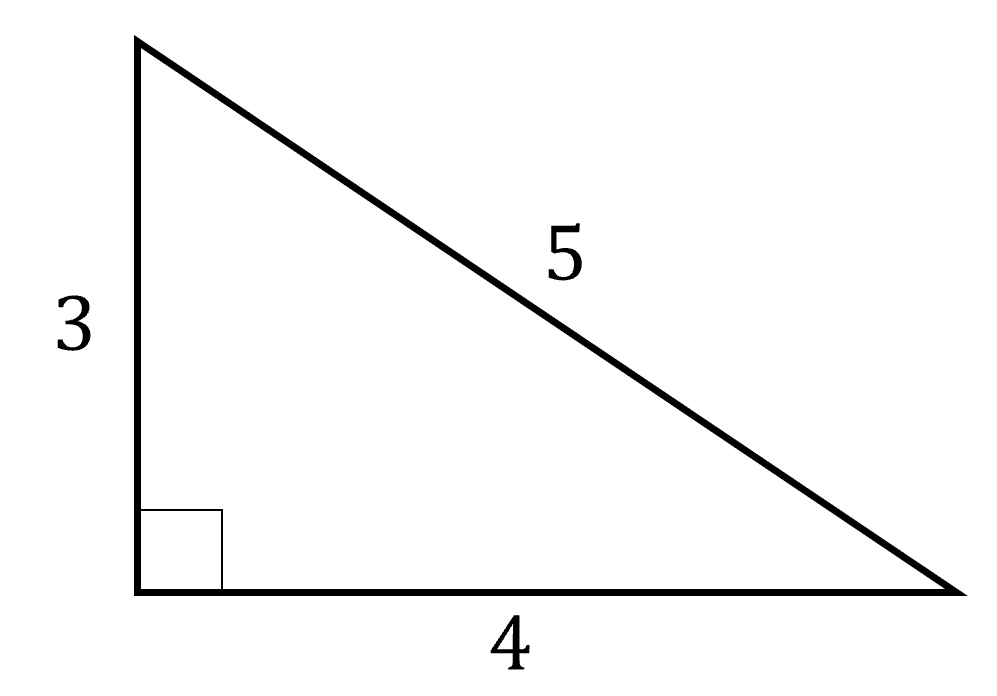
このことを利用して、古代エジプトでは直角を作っていたと言われています。
2 問題の確認
問題
原始ピタゴラス数は他にもあるのか。あるなら具体例を示せ。
原始ピタゴラス数は無数にあるのか。あるなら生成する式を、ないならばそれを証明せよ。
3 ピタゴラスの定理をよ~~~く見る
ここで再登場。ピタゴラスの定理です。
$${a^2+b^2=c^2}$$
ここで、この$${a,b,c}$$は直角三角形の1つの辺の長さでした。
では長さを2乗したピタゴラスの定理は、辺の長さについての式ではなく、面積についての式と言えます。(※)
どんな図形の面積かというと、一辺を2乗したのだから、正方形の面積ですね。(図4)
(※)
長さを2乗すると、面積になります。これは単位を見るとよく分かります。
長さの単位は$${m}$$ですが、面積の単位は$${m^2}$$のように、$${m}$$が2乗されるのです。

2つの正方形の面積を足して、1つの正方形の面積にする。
これをペットボトルキャップで表現してみる価値がありそうです。
4 ペットボトルキャップでの確かめ方法



5 キャップを使ってやってみる!!
・ 1辺の長さが2の正方形の場合

この場合、
①で一辺の長さが2の正方形を作り、
②で一辺の長さが3の正方形を作った。
数式で表すと、
$${2^2+b^2=3^2}$$
という形まで作っている。
あとは、図5の③のキャップで正方形を作れればいいのですが、できませんでした。(図6)

・ 周りに付け加えるキャップを増やす
下の図のように、周りに付け加えるキャップの数を増やせば、もしかしたら正方形を作れるかもしれません。
ここで、最初に付け加えた1組のキャップをまとめて1層、次に付け加えた1組のキャップを2層というように呼ぶこととします。

2層に増やした場合、このように正方形はできませんでした。

3層に増やしても、正方形はできませんでした。

これ以上層を増やしても、直感的にできそうにありません。(※)
なので、1辺の長さが3の正方形について考えてみましょう。
※ 証明は記事の最後に紹介しています。
・ 1辺の長さが3の正方形の場合

③を変形して正方形を作れるか。
残念ながら作れません。

層を増やしてみると、どうでしょう。

ようやくできました👏👏
6 見出した正方形が作れる条件
図12の変形で気づいたことがあります。
それは、最初に一辺の長さが3の正方形があった隙間に2層目のキャップを移動させれば正方形を作れたということです。(図13)

これを、もう少し一般的に表現すると、こうなります。
最初に一辺の長さが$${n}$$の正方形があったとする。
この正方形の周りにペットボトルキャップを付け加えたとき、第$${k}$$層のキャップの数と正方形のキャップの個数が一致すれば、必ず正方形を作ることができる。(図14)

7 おわりに
前編の記事では、ここまでとします。
次回の記事では、最後に見出した正方形を作れる条件を利用して、原始ピタゴラス数を見つけていきます。
・ ※の証明
1層、2層、3層のそれぞれのキャップの個数は5,7,9です。
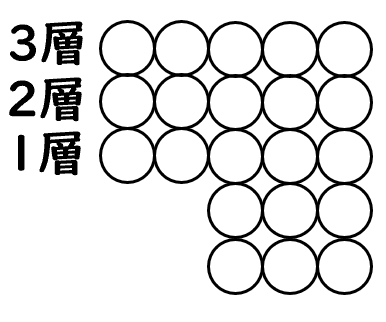
$${k}$$層までのキャップの個数の合計を$${S_k}$$とすると、
$${S_1=5}$$
$${S_2=5+7=12}$$
$${S_3=12+9=21}$$
です。
$${S_k}$$の一般項を求めると、
$${S_k=k^2+4k}$$
因数分解すると、
$${S_k=k(k+4)}$$
この右辺を見ると、明らか$${S_k}$$は平方数ではないので、正方形が作れないということになります。
後編はこちら↓↓
最後まで読んでいただき、ありがとうございました!!

