【東京工業大学2020年度前期入試数学第2問】作問の詰めの甘さを感じる図形問題

東京工業大学の全問チャレンジですが、第1問はすでに(批判とともに)紹介していますので、第2問です。今回も厳しめの評価です。

東京工業大学　本館
2011年5月19日、03撮影、Wikipediaより

[問題] 複素数平面上の異なる3点 A, B, C を複素数 α，β，γ で表す。ここで A, B, C は同一直線上にないと仮定する。
(1) △ABC が正三角形となる必要十分条件は，α^2 + β^2 + γ^2 = αβ + βγ + γα であることを示せ。
(2) △ABC が正三角形のとき，△ABC の外接円上に点 P を任意にとる。このとき，AP^2 + BP^2 + CP^2 および AP^4 + BP^4 + CP^4 を外接円の半径 R を用いて表せ。ただし 2点 X, Y に対し，XY とは線分 XY の長さを表す。

まず最初に、私の頃は複素数平面は受験対策として知ってはいましたが、学習指導要領にはない時代だったので、あまり複素数平面になじんでいません。

そのせいかもしれませんが、(1) と (2) がばらばらな問題に見えてしまいます。そのくらい、(2) は (1) と独立の問題になっています。少なくとも (1) の必然性が感じられません。

一応、解答してみますが、最初の (1) はどうとでもなる問題だと思います。

例えば単純な方法として、AB = AC かつ ∠A = 60° であるので、

(β - α) / (γ - α) = cos(±60°) + i sin(±60°) = (1/2) ± (√3/2)i

と表されます。ここで α ≠ γ に注意してください。このとき、1/2 を左辺に移項して、両辺を2乗するすることで、{(β - α) / (γ - α)}^2 - {(β - α) / (γ - α)} + (1/4) = -3/4 から (β - α)^2 - (β - α)(γ - α) + (γ - α)^2 = 0 が得られます。

この左辺を展開して整理すると、β^2 - 2αβ + α^2 - βγ + αβ + γα - α^2 + γ^2 -2γα + α^2 = 0 すなわち α^2 + β^2 + γ^2 - αβ - βγ - γα = 0となるので、

α^2 + β^2 + γ^2 = αβ + βγ + γα

が得られます。

逆に、α^2 + β^2 + γ^2 = αβ + βγ + γα が成立するとき、計算を逆にたどることにより、△ABC が正三角形であることが言えます。

この一言は必ず書いてください。必要十分条件であることを示せなので、この一言がなければ減点になります。

(2) ですが、複素数平面を完全に無視します。その方が簡単だと思います。

正三角形の外心は重心でもあります。これを G とおくと、GA = GB = GC = R であり、∠AGB = ∠BGC = ∠CGA = 120° となります。下図参照。

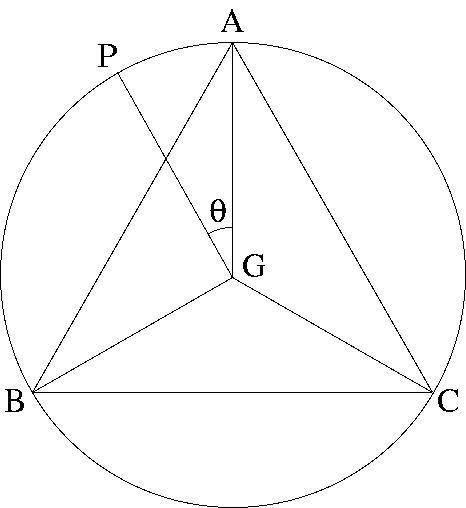
図形の対称性より外心円上の点 P が弧 AB 上にあると仮定して一般性を失いません。さらに一般性を失うことなく P は点B より点 A に近い(もしくは距離が等しい)と仮定します。また、∠AGP = θ とおきます(このとき 0° ≦ θ ≦ 60° です)。

このとき、余弦定理(180° まで成立することに注意)より
・AP^2 = GA^2 + GP^2 - 2GA・GP cos θ = 2R^2 -2R^2 cos θ
・BP^2 = GB^2 + GP^2 - 2GB・GP cos(120° - θ) = 2R^2 -2R^2 cos(120° - θ)
・CP^2 = GC^2 + GP^2 - 2GA・GP cos(120° + θ) = 2R^2 -2R^2 cos(120° + θ)
が得られます。これらをたすと

AP^2 + BP^2 + CP^2 = 6R^2 -2R^2 {cos θ + cos(120° - θ) + cos(120° + θ)}

となります。ここで、次の補題を証明します。

[補題] cos θ + cos(120° - θ) + cos(120° + θ) = 0

[補題の証明] cos θ + cos(120° - θ) + cos(120° + θ) = cos θ + cos 120° cos θ + sin 120° sin θ + cos 120° cos θ - sin 120° sin θ = cos θ - (1/2)cos θ - (1/2)cos θ = 0 [証明終]

この補題を用いると、AP^2 + BP^2 + CP^2 = 6R^2 が得られます。

さらに、AP^4 + BP^4 + CP^4 については、
・AP^4 = (AP^2)^2 = 4R^4 (1 - cos θ)^2 = 4R^4(1 - 2cos θ + cos^2 θ)
・BP^4 = (BP^2)^2 = 4R^4 {1 - cos(120° - θ)}^2 = 4R^4{1 - 2cos(120° - θ) + cos^2(120° - θ)}
・CP^4 = (CP^2)^2 = 4R^4 {1 - cos(120° + θ)}^2 = 4R^4{1 - 2cos(120° + θ) + cos^2(120° + θ)}
が成立するので、すべて足すと補題から AP^4 + BP^4 + CP^4 = 4R^4 × {3 + cos^2 θ + cos^2(120° - θ) + cos^2(120° + θ)} が得られます。

ここで、加法定理で 120° ± θ をばらすと、cos^2 θ + cos^2(120° - θ) + cos^2(120° + θ) = 3/2 となります(少し面倒ですが難しい計算ではありません)。

よって、AP^4 + BP^4 + CP^4 = 4R^4 × {3 + cos^2 θ + cos^2(120° - θ) + cos^2(120° + θ)} = 4R^4 × {3 + (3/2)} = 18R^2 が得られます。

見ての通り、複素数平面を用いずに簡単に解けます。むしろ、(1) を用いた方が難しくなるのではないかと思います。簡単な解法があるでしょうか？

この辺りは別解の調査がなってないような気がして、作問の詰めが甘いと言わざるを得ません。もちろん、作問ミスではないので記者会見で謝罪という話ではないのですが。

第1問といい、第2問といい、ここまでの段階では作問担当者の仕事ぶりは感心しません。