【名古屋大学2021年度前期入試数学(理系)第4問】ちょっと丁寧すぎる？漸化式の問題

名古屋大学最後の問題は、漸化式にガウス記号が出てきてビビるかもしれませんが、実際には誘導問題が丁寧すぎるためにそれほど難しくはないです。

名古屋大学東山キャンパス
2016年4月17日、DrKssn撮影、Wikipediaより

問題

0 ≦ a < 1 を満たす実数 a に対し，数列 {a(n)} を

a(1) = a，a(n+1) = 3[a(n) + (1/2)] - 2a(n)　　　(n = 1, 2, 3, ...)

という漸化式で定める。ただし，[x] は x 以下の最大の整数を表す。以下の問に答えよ。

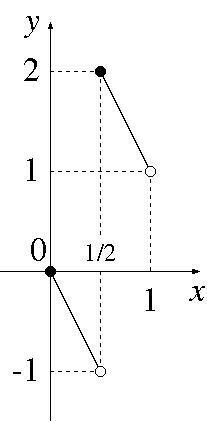
(1) a が 0 ≦ a < 1 の範囲を動くとき，点 (x, y) = (a(1), a(2)) の軌跡を xy 平面上に図示せよ。

(2) a(n) - [a(n)] ≧ 1/2 ならば，a(n) < a(n+1) であることを示せ。

(3) a(n) > a(n+1) ならば，a(n+1) = 3[a(n)] - 2a(n) かつ [a(n+1)] = [a(n)] - 1 であることを示せ。

(4) ある 2 以上の自然数 k に対して，a(1) > a(2) > … > a(k) が成り立つとする。このとき a(k) を a の式で表せ。

(注) いつも通り、a(n) は原文では添え字 n がついている a を表しているとします。

解答解説

(1) が何のためにあるのか分からないですが、まあ、基本的には誘導に乗って何も考えずに進めることです。

とにもかくにも、[a(n) + (1/2)] の部分がどうなるかで場合分けするしかないわけで、逆に言えば、それが唯一の方針と言ってもいいでしょう。

(1) は a(n) のところに a(1) = a が入るわけですから、0 ≦ a < 1/2 と 1/2 ≦ a < 1 で場合分けすることがすぐに分かると思います。

0 ≦ a < 1/2 のときには 1/2 ≦ a + (1/2) < 1 なので、[a + (1/2)] = 0 となります。したがって、a(2) = 3[a(1) + (1/2)] - 2a(1) = -2a(1) となるので、y = -2x (0 ≦ x < 1/2) が得られます。

1/2 ≦ a < 1 のときには 1 ≦ a + (1/2) < 3/2 なので、[a + (1/2)] = 1 となります。したがって、a(2) = 3[a(1) + (1/2)] - 2a(1) = 3 - 2a(1) となるので、y = -2x + 3 (1/2 ≦ x < 1) が得られます。

ということで、下図が得られます。(黒丸は軌跡に含まれ、白丸は軌跡に含まれません。)

(2) は条件を素直に使うことです。仮定と [x] の定義から 1/2 ≦ a(n) - [a(n)] < 1 なので、[a(n)] + 1 ≦ a(n) + (1/2) < [a(n)] + (3/2) となります。ここで [a(n)] は整数なので、[a(n) + (1/2)] = [a(n)] + 1 となります。

このとき、a(n+1) = 3[a(n) + (1/2)] - 2a(n) = 3[a(n)] + 3 - 2a(n) が得られます。ここで a(n) - [a(n)] < 1 を用いると、a(n+1) - a(n) = 3[a(n)] - 3a(n) + 3 = 3 - 3(a(n) - [a(n)]) > 3 - 3 × 1 = 0 であるので、a(n) < a(n+1) が成立します。

(3) は (2) の対偶を使うことがすぐに分かると思います。a(n) > a(n+1)  であるとき、(2) と [x] の定義から 0 ≦ a(n) - [a(n)] < 1/2 が成立します。このとき、[a(n)] + (1/2) ≦ a(n) + (1/2) < [a(n)] + 1 で、[a(n)] は整数なので、[a(n) + (1/2)] = [a(n)] となります。

よって、a(n+1) = 3[a(n) + (1/2)] - 2a(n) = 3[a(n)] - 2a(n) が示されました。

さてここで、a(n) = [a(n)] と仮定すると、a(n+1) = 3a(n) - 2a(n) = a(n) となり、a(n) > a(n+1) に反するので、a(n) > [a(n)] すなわち 0 < a(n) - [a(n)] < 1/2 が得られます。

これを a(n+1) = [a(n)] - 2{a(n) - [a(n)]} に用いると、[a(n)] - 1 < a(n+1) < [a(n)] が成り立つので、[a(n)] が整数であることより [a(n+1)] = [a(n)] - 1 が示されました。

(4) は (3) を使えばいいことが分かると思います。2つの式を用いると、n = 1, 2, ..., k - 1 に対して

a(n+1) - [a(n+1)] = -2 {a(n) - [a(n)] } + 1

が成り立ちます。b(n) = a(n) - [a(n)] とおくと、b(n+1) = -2b(n) + 1 すなわち b(n+1) - (1/3) = -2 {b(n) - (1/3)} が得られるので、n = 1, 2, ..., k に対して b(n) = {b(1) - (1/3)}・(-2)^{n-1} + (1/3) となります。

ここで、b(1) = a(1) - [a(1)] で、0 ≦ a(1) = a < 1 であるので、b(1) = a - 0 = a となり、b(n) = a(n) - [a(n)] = (a - (1/3))・(-2)^{n-1} + (1/3) となります。

次に、[a(n+1)] = [a(n)] - 1 から、[a(n)] は初項 [a(1)] = 0、公差 -1 の等差数列となるので、[a(n)] = -n + 1 となり、これを先ほどの式に代入することで、a(n) = (a - (1/3))・(-2)^{n-1} - n + (4/3) が求まります。n = k を代入して、答えは a(k) = (a - (1/3))・(-2)^{k-1) - k + (4/3) となります。

感想

漸化式の中にガウス記号があることで敬遠したくなるかもしれませんが、実際に手を出してみると簡単に解けます。こういう問題は見かけに騙されないことです。

「簡単」とは書きましたが、きちんと入試レベルの問題ではあって、決して教科書の演習問題レベルではないので、受験生の間でそれなりに差がつくように思います。そういう意味では適切な問題だと思いました。