【東京工業大学2021年度前期入試数学第5問】計算が面倒な回転体の問題

最後は回転体の問題です。簡単ですが、計算がちょっとうっとうしいです。

東京工業大学　本館
2011年5月19日、03撮影、Wikipediaより

問題

xy 平面上の円 C : (x^2) + (y - a)^2 = (a^2)　(a > 0)　を考える．以下の問いに答えよ．

(1) 円 C が y ≧ x^2 で表される領域に含まれるための a の範囲を求めよ．

(2) 円 C が y ≧ (x^2) - (x^4) で表される領域に含まれるための a の範囲を求めよ．

(3) a が (2) の範囲にあるとする．xy 平面において連立不等式
　|x| ≦ (1/√2)，0 ≦ y ≦ (1/4)，y ≧ (x^2) - (x^4)，(x^2) + (y - a)^2 ≧ (a^2)
で表される領域 D を，y 軸の周りに 1回転させてできる立体の体積を求めよ．

解答解説

手を動かしてみればどうにかなると思います。

まず、円の式を x^2 = (a^2) - (y - a)^2 = 2ay - (y^2) に変形しておきます。ここで、0 ≦ y ≦ 2a であることに注意してください。

(1) は y ≧ x^2 に円の式を代入して y の式を出します。

y ≧ 2ay - (y^2) すなわち、y(y - 2a + 1) ≧ 0

これが 0 ≦ y ≦ 2a に対して常に成り立つ必要があるため、y ≧ 0 であることから、y - 2a + 1 ≧ 0 が常に成り立てばいいことになります。

この左辺は y の増加関数であるため、y = 0 のときに成り立てばよく、-2a + 1 ≧ 0 すなわち 0 < a ≦ 1/2 が求める範囲になります。

(2) も同じように考えます。y ≧ (x^2) - (x^4) に円の式を代入します。

y ≧ {2ay - (y^2)} - {2ay - (y^2)}^2
すなわち
y × {(y^3) - 4a(y^2) + {4(a^2) + 1}y - (2a - 1)} ≧ 0

これが 0 ≦ y ≦ 2a の範囲で満たされればよいので、次の式が満たされればよいことになります。

(y^3) - 4a(y^2) + {4(a^2) + 1}y - (2a - 1) ≧ 0

左辺を f(y) とおきます。すなわち、f(y) = (y^3) - 4a(y^2) + {4(a^2) + 1}y - (2a - 1) とおきます。

まず、f(0) = - (2a - 1) ≧ 0 であることから、(0 <) a ≦ 1/2 が得られます。

次に、f を微分すると、f'(y) = 3(y^2) - 8ay + 4(a^2) + 1 = 3{y - (4a/3)}^2 + 1 - (4a^2/3) となりますが、a ≦ 1/2 であるとき、1 - (4a^2/3) ≧ 1 - (1/3) = 2/3 > 0 となるので、f'(y) > 0 であり、f(y) は増加関数となります。

よって、f(0) ≧ 0 であるとき、0 ≦ y ≦ 2a の範囲で f(y) ≧ f(0) ≧ 0 となるため、0 < a ≦ 1/2 という範囲が得られます。

(3) は最初に y = (x^2) - (x^4) を書いてみます。dy/dx = 2x - 4x^3 = 2x(1 - 2x^2) であるので、次のような図形になります。

実は、|x|=1/√2 のときに f(x) が最大となり、最大値は f(±1/√2) = 1/4 です。この点に注意してください。

ではまず、連立不等式で定義される領域 D' を y 軸の周りに 1回転してできる体積を求めます。

|x| ≦ (1/√2)，0 ≦ y ≦ (1/4)，y ≧ (x^2) - (x^4)

そのために、y = (x^2) - (x^4) を x^2 について解きます。

すると、(x^2)^2 - (x^2) + y = 0 から x^2 = {1 ± √(1 - 4y)}/2 が出てきます。ここで、{1 + √(1 - 4y)}/2 ≧ 1/2 であることから、領域 |x| ≦ (1/√2)，0 ≦ y ≦ (1/4) の範囲にあるのは x^2 = {1 - √(1 - 4y)}/2 となります。

よって、D' を y 軸の周りに 1回転してできる体積は次のようになります。

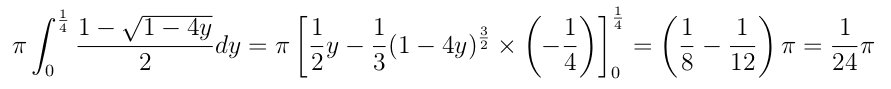
さて、D を y 軸の周りに 1回転してできる図形の体積は、D' を y 軸の周りに 1回転してできる図形の体積から円 C を回転させた部分の体積を引いて求められます。

0 < a ≦ 1/8 のとき、円 C はすべて 0 ≦ y ≦ 1/4 に含まれるので、求める体積は上記の体積から半径 a の球の体積を引いたとなるので、(π/24) - (4/3) π(a^3) となります。

1/8 ≦ a ≦ 1/2 のとき、下のグラフのように円が y > 1/4 の部分にかかるため、引かれる部分の体積は次のようになります。

よって、求める体積は (π/24) - {(a/16) - (1/192)}π = {(3/64) - (a/16)}π となります。

感想

最後の問題も取り立てて難しい問題ではないと思います。(1) がなぜあったのか分かりませんが、(2) は (3) で面倒なケースを排除するための設問だったと思います。本質的には (3) が主題でしょう。

全5問が終わりましたが、あまり難しい問題はないように感じます。計算量もさほどあるわけではないので、満点を取ることも難しくないのではないでしょうか？