【一橋大学2021年度前期入試数学第2問】よく見れば等差数列×等比数列の和

今年度の一橋の第2問はタイトルの通り、等差数列×等比数列の和という基本的な問題が姿を変えて出てまいりました。

一橋大学　兼松講堂
2008年9月20日、Wiiii撮影、Wikipediaより

問題

実数 x に対し，x を超えない最大の整数を整数を [x] で表す。数列 { a(k) } を
　　　　　a(k) = 2^{[√k]}　　(k = 1, 2, 3, ...)
で定義する。正の整数 n に対して
　　　　　b(n) = Σ_{k=1}^{n^{2}} a(k)
を求めよ。

(注) いつも通り、a(k) と b(n) はそれぞれ a に下付き文字のk と b に下付き文字の n です。

解答解説

k を正の整数とし、i を i^{2} ≦ k ≦ (i + 1)^{2} -1 を満たす整数とすると、i ≦ √k < i + 1 であるので、[k] = i であり、a(k) = 2^{i} となります。よって、n ≧ 2 のときには

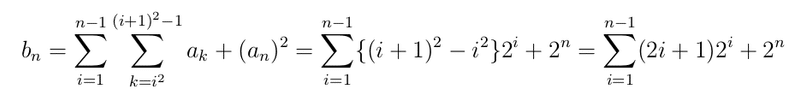
が得られます。ここで、

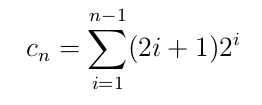
とおくと、

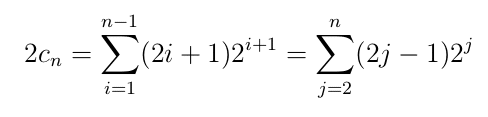
であることから、

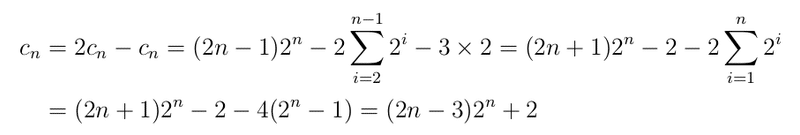
が得られます。よって、b(n) = (2n - 3) × 2^{n} + 2 + 2^{n} = (2n - 2) × 2^{n} + 2 = (n - 1) × 2^{n+1} + 2 となります。この式は n = 1 のときにも成立しています。

感想

指数の肩にルートが乗って大変と思いきや、[√k] が一定である範囲に分けてあげると簡単に整理ができて、b(n) は実質的に等差数列×等比数列の和になっているという、教科書に出てくるタイプの問題に落とし込むことができます。

普通の年であれば「バカにするのも大概にしろ！」と言うのでしょうけれども、コロナ禍では仕方がないのかなぁ…と。

でも、コロナ禍だから逆に学校に煩わされることなく受験に専念できたと見ることもできるのですが、その辺りはどうなんでしょう？

やっぱり、コロナ禍と言えどもこれは易しすぎではないかと思わずにはいられません。