【渋谷教育学園幕張中学校2020年度入試算数第4問】これいいの？な平面図形問題

今回は図形問題ですが、何というか、(1) と (2) は難関中学校としてはありがちな問題ですが、(3) については物議をかもすと思います。(2) が誘導問題になっているとはいえ、本質的に√3 を使っています。ホントにいいのでしょうか？苦笑

渋谷教育学園幕張中学校・高等学校
2008年6月20日、Kattin撮影、Wikipediaより

問題

次の各問いに答えなさい。ただし，図は正確とは限りません。

(1) 図1 のように直角三角形 ABC に AC を1辺とする正方形と BC を1辺とする正方形をかき，2つの点 D, E を直線で結びます。このとき，三角形 CDE の面積は何 cm2 ですか。

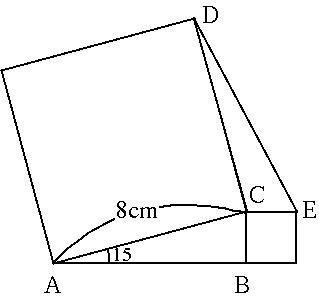
図1

(2) 図2 のような直角三角形 ABC と，AD, BD, CD をそれぞれ1辺とする正方形があります。このとき，CD を1辺とする正方形の面積は何 cm2 ですか。

図2

(3) AB = AD，AD : DC = 2 : 3，角 A の大きさが 150°，角 D の大きさが 90° である四角形 ABCD があります。辺 BC をのばしたところに2つの点 E, F をとります。次に，直角三角形 AEG と 直角三角形 DFH をかいたところ，図3 のようになりました。直線 AD と直線 GH が平行のとき，三角形 ABE の面積は三角形 DCF の面積の何倍ですか。

図3

解答解説

まず最初に次の図を考えてみます。

ここで、α + β = 180° とします。また、2つの角をはさむ辺がそれぞれ a : b と c : d であったとします。
(ここで、b と c および a と d には関係がなくてかまいません。)

このとき、2つの三角形の面積の比は 左 : 右 = a × c : b × d となります。理由は、a と b の辺が底辺だとみなすと、2つの三角形の高さの比が c : d になるからです。

実は (1) はそれを踏まえた問題になっていますが、(3) でも重要な役割をはたします。

(1) は結局、角 ACB + 角 DCE = 180°、AC = DC = 8cm、BC = EC であるので、面積を比較すると三角形 ABC : 三角形 CDE = 1 : 1 すなわち 三角形 ABC = 三角形 CDE となります。

ここで、三角形 ABC は有名な三角形で、8 × 4 ÷ 2 ÷ 2 = 8cm2 となるので、三角形 CDE = 8cm2 が得られます。

(2) はもう少し簡単です。中学生であれば CD = √3 なので、CD を1辺とする正方形の面積は √3 × √3 = 3 と求まりますが、ここは小学生です。平方根は知りません。

ということで、三角形 ACD と三角形 CBD を比較します。この2つの三角形は高さが CD と共通で、底辺が AC : CD = 1 : 3 なので、三角形 ACD : 三角形 CBD = 1 : 3 となります。

もう一つ重要なことは、三角形 ACD と三角形 CBD は相似だということです。なので、AD × AD : CD × CD = 三角形 ACD : 三角形 CBD = 1 : 3 となり、AD × AD = 1 なので、CD を1辺とする正方形の面積 = CD × CD = 3cm2 となります。

さて、物議をかもす (3) です。

30°、60°、90° の直角三角形の辺の比を 1 : 2 : ■ とおいておきます。先ほどの結論から ■ × ■ = 3 です。これを使います。√3 の代わりに ■ とおいているだけです。いいのでしょうか？

まず、三角形 ABE と 三角形 ADG について考えます。角 EAG = 30° かつ角 BAD = 150° であるので、角 BAE + 角 DAG = 360° - (30° + 150°) = 180° で、AB = AD かつ AE : AG = 2 : ■ なので、三角形 ABE : 三角形 ADG = 2 : ■ になります。

次に、三角形 DCF と 三角形 DAH について考えます。角 ADC = 角 HDF = 90° であるので、角 CDF + 角 ADH = 360° - (90° + 90°) = 180° で、CD : AD = 3 : 2 かつ DF : DH = ■ : 1 なので、三角形 DCF : 三角形 DAH = 3 × ■ : 2 × 1 になります。

最後に、三角形 ADG と 三角形 DAH ですが、どちらも底辺は AD で、残りの点 GH を結んだ直線は AD に平行なので、2つの三角形の高さは等しくなります。したがって、三角形 ADG = 三角形 DAH となります。

以上のことから、三角形 ABE = (2/■) × 三角形 ADG = (2/■) × 三角形 DAH = (2/■) × { 2/(3 × ■) } × 三角形 DCF = { (2 × 2)/(■ × 3 × ■) } × 三角形 DCF = (4/9) × 三角形 DCF となります。

最初と最後だけにすると、

三角形 ABE = (4/9) × 三角形 DCF

ということで、三角形 ABE の面積は三角形 DCF の面積の 4/9 倍です。

私の中ではこの解答しか作れません。問題ですが、

√3 を使わない解答が渋幕にはあるのでしょうか？

私はないと予想しています。もしあるならばお目にかかりたいので、ぜひ渋幕には解答案を公表していただきたい。

中学入試はとかくやりがちな面がありますが、一応、小学校の算数の範囲内という前提があります。その前提をあからさまに破るのはさすがにNGです。

ルールを破っていいのであれば、極端な話、中学入試で微分積分を出してもよくなってしまいます。もちろん、そんなバカな話はありません。

第2問といい、問題自体は非常に面白いし、中学入試を抜きにすれば私は好きですが、中学入試としてはさすがにNGです。そしておそらく、意図的にやっているという意味で渋幕の入試は冗談がきついと断罪せざるを得ません。