【一橋大学2021年度前期入試数学第4問】難しくはないけど入試らしい問題

今回は2次曲線の問題です。丁寧に解いていけば難しくないですが、何と言いますか…入試らしい入試問題です。

一橋大学　兼松講堂
2008年9月20日、Wiiii撮影、Wikipediaより

問題

k > 0 とする。円 C を (x^2) + (y - 1)^2 = 1 とし，放物線 S を y = (1/k)(x^2) とする。

(1) C と S が共有点をちょうど3個持つときの k の範囲を求めよ。

(2) k が (1) の範囲を動くとき，C と S の共有点のうちで x 座標が正の点を P とする。P における S の接線と S と y 軸とによって囲まれる領域の面積の最大値を求めよ。

解答解説

やっと入試らしい入試問題が登場した気がします。

(1) は S の式で C の式の y を消去しましょう。すると、(x^2) + {(1/k)(x^2) - 1}^2 = 1 から (1/k^2)x^4 + {1 - (2/k)}x^2 = 0 すなわち (1/k^2)(x^2){(x^2) + k(k - 2)} = 0 が得られます。

この方程式が 3 個の(異なる)実数解を持つための条件は k(k - 2) < 0 となることですが、k > 0 であることから、(0 <) k < 2 が得られます。

(2) は、P の x 座標を求めると x = √{k(2-k)} となります。ここで、p = √{k(2-k)} とします。

ここで、x = p における S の接線の方程式を y = f(x) とおき、g(x) = (1/k)(x^2) - f(x) とおくと、g(x) = (1/k)(x - p)^2 となるため、求める面積 A は

A = ∫_{0}^{p} g(x) dx = {1/(3k)} × [(x - p)^3]_{0}^{p} = (p^3)/(3k) = √{k(2 - k)^3}/3

となります。ここで、h(k) = k(2 - k)^3 とおくと、A = √h(k)/3 となるため、h(k) が最大のときに A も最大となります。

h'(k) = (2 - k)^3 - 3k(2 - k)^2 = 2(1 - 2k)(2 - k)^2 となるので、以下のような増減表が得られ、0 < k < 2 の範囲では k = 1/2 のときに h(k) は最大値 h(1/2) = 27/16 を取ります。

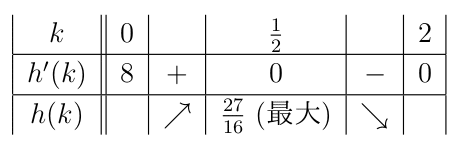
よって、面積は k = 1/2 のときに最大となり、最大値は √(27/16) / 3 = √3/4 となります。

感想

問題そのものは難しくないかもしれませんが、いかにも入試問題という感じがします。

面積を求める部分は、放物線と直線が接する＝二つの方程式から得られる x の二次方程式が重解を持つ、ということで、(1/k)(x - p)^2 としてあげると式が簡単になります。知っておくといいでしょう。というか、基本です。