【渋谷教育学園幕張中学校2020年度入試算数第2問】小学生版整数問題

今回の問題は大変面白い問題で、入試でなければ何も言うことはないのですが、 (4) については完全に数学の範囲になってしまっていて入試としては悩ましいところです。

渋幕側が果たして小学生にどこまでの能力を求めているのか、ちょっとすっきりしないところです。

渋谷教育学園幕張中学校・高等学校
2008年6月20日、Kattin撮影、Wikipediaより

問題

黒い正方形のわりに 1辺の長さが 1cm の白い正方形を並べます。下の図は，左から 1辺の長さが 1cm, 2cm, 3cm, …… の黒い正方形のまわりに白い正方形を並べたものです。

図

白い正方形のマスの中に，1は1個，2は2個，3は3個，…… のように整数 A は A 個使い、ある整数から連続した 2種類以上の整数を並べます。

たとえば，図1の左側のように，黒い正方形の 1辺の長さが 2cm のとき，3を3個，4を4個，5を5個使うと，ちょうど並べることができます。しかし，図1の右側のように，4を4個，5を5個，6を6個ではちょうど並べきることができません。また，図2のように，黒い正方形の 1辺が 8cm のときは，１から8までと，11から13までの整数をちょうど並べきることができます。

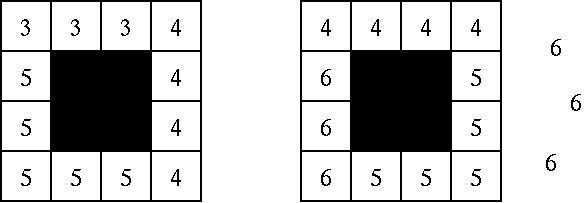
図1

図2

このとき，次の各問いに答えなさい。
ただし，(2), (3) では考えられるものを「○～○」のように書きなさい。たとえば，図1の左側の場合は，「3～5」，図2の場合は，「1～8と11～13」と表すことにします。

(1) 黒い正方形の 1辺の長さにかかわらず，連続した2種類の整数だけでは白い正方形のマスの中に整数をちょうど並べきることができません。その理由を説明しなさい。

(2) 黒い正方形の 1辺の長さが 9cm のとき，白い正方形のマス目の中に整数をちょうど並べきるには，いくつからいくつまでの整数を並べればよいですか。考えられるものをすべて答えなさい。

(3) 黒い正方形の 1辺の長さが 14cm のとき，白い正方形のマス目の中に整数をちょうど並べきるには，いくつからいくつまでの整数を並べればよいですか。考えられるものをすべて答えなさい。

(4) 黒い正方形の 1辺の長さが 100cm までの中で，白い正方形のマスの中に整数をちょうど並べきることができないのは，黒い正方形の 1辺の長さが何 cm のときですか。考えられるものをすべて答えなさい。

解答解説

猛烈に問題が長くなって頭が痛くなりそうですが、問題そのものは (4) をのぞけば難しくはありません。少しの観察力が必要なだけです。

1つ目は黒い正方形の 1辺の長さにかかわらず、白い正方形の個数が4の倍数になることです。正確に言うと、白い正方形の個数は　(黒い正方形の 1辺の長さ) + 1 を 4倍した数　になります。

2つ目は連続する2つの数をたすと奇数になるという事実です。なぜならば、偶数＋奇数は奇数になるからです。

3つ目は連続する整数をたすとどうなるかです。連続する整数の最初の数字と最後の数字を使うと

連続する整数の和 ＝ (最初の数 + 最後の数) × (最後の数 - 最初の数 + 1) ÷ 2

で表すことができます。ここで
・最初の数 + 最後の数
・最後の数 - 最初の数 + 1
の偶奇が異なることに注意してください。そうすると、2 × (連続する整数の和) を 2つの整数の積で表したときに一方は奇数でなければならなくなります。(もう一方は自動的に偶数になる。)

また、最初の数が 1 以上で、最後の数 > 最初の数であるためには

最初の数 + 最後の数 > 最後の数 - 最初の数 + 1 ≧ 2

でなければいけなくなります。(逆にそのように分ければ自動的に答えが求まります。)

このくらいのことが分かると問題を解くのに十分でしょう。

(1) はすでに答えが出ています。

白い正方形のマスの個数は4の倍数になるが、連続する2つの整数の和は偶数 + 奇数 = 奇数となるために4の倍数にならないから。

くらいでいいかと思います。

(2) は 2 × (白い正方形のマスの個数) = 2 × (9 + 1) × 4 = 80 = 16 × 5 であるので、
・最初の数 + 最後の数 = 16
・最後の数 - 最初の数 + 1 = 5
となり、最初の数 = 6 かつ 最後の数 = 10 すなわち 6～10 となります。

(3) も同じように考えていきます。2 × (白い正方形のマスの個数= 2 × (14 + 1) × 4 = 120 = 8 × 3 × 5になります。これは 3 つの場合があります。

① 8 と 15 に分ける場合
・最初の数 + 最後の数 = 15
・最後の数 - 最初の数 + 1 = 8
となり、最初の数 = 4 かつ 最後の数 = 11 すなわち 4～11 となります。

② 24 と 5 に分ける場合
・最初の数 + 最後の数 = 24
・最後の数 - 最初の数 + 1 = 5
となり、最初の数 = 10 かつ 最後の数 = 14 すなわち 10～14 となります。

① 40 と 3 に分ける場合
・最初の数 + 最後の数 = 40
・最後の数 - 最初の数 + 1 = 3
となり、最初の数 = 19 かつ 最後の数 = 21 すなわち 19～21 となります。

以上のことから、4～11と10～14と19～21が答えとなります。

(4) は 2 × 4 × (黒い正方形の1辺の長さ + 1) を 奇数 × 偶数 に分けたときに奇数が3以上であれば (2) や (3) のように解を求めることができます。

逆に、2 × 4 × (黒い正方形の1辺の長さ + 1) が 2 × 2 × … × 2 の形のときには2種類以上の連続する整数の和で表現することはできません。

ということで、黒い正方形の1辺の長さが 2 × 2 × … × 2 - 1 という形をしているときに実現できないので、1, 3, 7, 15, 31, 63 の6つ存在します。

今回の問題は、最初に解いた方法を捨てて、一番わかりやすいと思われる解答をのせています。

初見のときにはもっと泥臭い方法で求めています(もちろん、げんみつに求めています)。算数と数学を区別しているので、別ルートを取らざるを得ないこともありますので。

しかし、実際にはどちらの方法をとっても数学になってしまうので、それならばじゃっかん数学的なアプローチでもシンプルな方をのせることにしました。

この問題の (4) は不可能性を論じており、明確に数学の範囲に入ります。

ちなみに算数は答えを求めることが重視され、数学はその理屈が要求されます。もちろん、算数でも理屈は重要ですが、それを表立って要求はしない。だから、入試の算数では基本的に答えだけを要求しています。

(4) はその数がどのような連続した数の和にも表現できないことを示す必要があり、これは具体的な計算では求められず、議論でしか求められません。ですので数学なのです。

しかし、どこまで受験生は正確に議論できてるのでしょう？と不思議に思ってしまいます。

一方で、実際にはいろいろと試すことで黒い正方形の1辺の長さが 2 × 2 × … × 2 - 1 という形をしているときに実現できないという答えにたどりつくと思います。

解答らんには答えを得るまでの道すじを書く必要はないので、受験生としてはそれでいいのでしょうけど、数学の問題を出しておいて答えを出せればそれでいいという姿勢が果たして今後の数学教育に対していいのかは疑問が残るところです。

渋幕側の解答案を公表していただきたいなぁ…と、ちょっと思ってしまいます。