統計的検定を理解するのに大事なポイント

普段、テスト理論とよばれる統計的な手法を応用した学力テストや心理尺度の開発、マーケティングデータの分析、社会人の方向けの統計の教育などに取り組んでいます。こちらのページに、統計やデータサイエンス、テストの開発について、よくいただくご質問に対する説明を少しずつまとめて行きます。よろしくお願いします。

はじめに

心理学の研究ではt検定やF検定などの『統計的検定』がよく使われます。最近は広告のABテストのように企業のマーケティング領域でも統計的な検定が活用されています。

一方で、『統計的検定』については「頻繁に目にする割に、どういうものなのかよくわからない」、「なんとなくは知っているけれども、正確に理解しているか自信がない」という声をよく耳にします（正直にいうと、自分自身もよく混乱します）。

実際『統計的検定』の考え方は、結構込み入った部分もあるのですが、自分なりにできるだけわかりやすく本質的な部分を解説してみます。

おそらく実際に一番よく利用される『統計的検定』は、2群間の平均値の差についのt検定だと思いますが、平均値差の検定は（名前の通り）2つのグループについて考える必要があって複雑なので、平均値差のt検定についても後で見ることにして、まずよりシンプルな相関係数の場合の『統計的検定』がどういうものか確認します。
（統計的検定を最初に利用するのが，2群間の差の検定という比較的複雑なケースになっていることが，実は統計的検定の理解を妨げる大きな要因になっているのではないかという気がしています）。

『統計的検定』の考え方を理解する上で、重要なポイントは次の3つです。

Point1. 何度もデータを取り直せるとしたら、サンプルの統計的な指標は毎回異なった値になる

Point2. 母集団の統計的な指標がゼロだと仮定した場合のサンプルでの指標の分布を考える

Point3. 母集団における統計的な指標が仮にゼロの場合に、手元にあるデータよりも極端な数値が発生する確率を計算する

これらを順に見ていくことで、統計的検定がどういうものか、かなり深いレベルで理解できると思います。

ポイント1 何度もデータを取り直せるとしたら、サンプルの統計的な指標は毎回異なった値になる

下の図は相関が0.5の2つの変数のデータです。架空のデータですが、たとえば横軸が性格検査の外向性のスコアを、縦軸が1日の発話量を、点の一つ一つが個人を表していると考えてください。また、人数は十分に大きいものとします。

このグラフは母集団全体を表したものですが、ここからランダムに10人を抜き出してサンプルの相関係数を計算します。実際に3回繰り返してみたところ、結果は次のようになりました。

同じ相関0.5の母集団から抽出したサンプルでも、相関係数は0.68、0.38、0.76と毎回違った値になっています。通常、母集団からランダムにサンプルを取り出すと、サンプルの相関係数は毎回異なった値となります。また、母集団の相関係数とサンプルの相関係数はほとんどの場合一致しません。これが第１のポイントです。あたり前の話のようですが、このことが『統計的検定』の考え方のベースになっています。

ポイント2 母集団の統計的な指標がゼロだと仮定した場合のサンプルでの指標の分布を考える

では，『相関係数がゼロの母集団から10人のサンプルを取り出して相関係数を計算する』ということをできるだけ多くの回数，たとえば10万回実行したら、どのような結果が得られるでしょうか．実際にやってみます。

母集団の相関係数はゼロとしてサンプルを10万回取り出してその都度相関係数を計算すると10万個の相関係数が得られます。これを整理して，横軸に相関係数の大きさ、縦軸に出現回数を取ったヒストグラムにまとめたのが次のグラフです。

相関係数なので横軸の値は-1から1の範囲になっています。縦軸は10万回のうちの頻度を表しています．0.0付近がピークのきれいな山形になっていますが、0.5よりも大きい値も見られます。母集団の相関係数がゼロであっても、サンプル数が10人程度場合にはサンプルの相関係数が（たまたま）0.5を超えるようなことも珍しくはないことがわかります。

一般にサンプルサイズをnとして『母集団の相関係数がゼロだと仮定した場合のサンプルサイズn（人）の相関係数の分布』が、コンピュータを使ったシミュレーションや理論的な検討などによって，このような形で具体的に把握できるということを知っておいてください。

参考に、相関が0.3の母集団から10人を取り出した場合の分布、相関がゼロの母集団から100人を取り出した場合の分布についても、それぞれ見てみます。
下の図は相関が0.3の母集団から10人を取り出した場合の分布です。ピークが右にシフトした形状になっています。

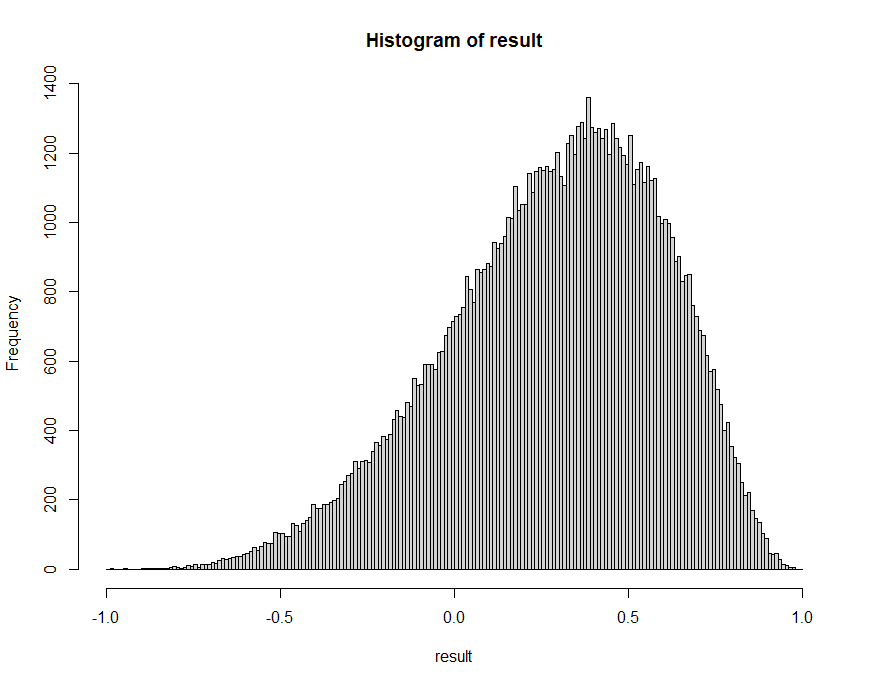
次の図は、相関係数がゼロでサンプルの人数を100人にした場合です。サンプルが増えると分布の幅が狭くなることがわかります。

いま、確認のために相関係数が0.3の場合の分布も見てみましたが、『統計的検定』で大事なのは母集団の相関係数がゼロの場合の分布です。

※ここで出てくる『母集団から取り出したサンプルでの計算結果の分布』という考え方は他の多くの統計的な手法でも重要になるのですが，なかなかイメージをつかむのが難しく，多くの人がつまづきやすいポイントでもあるように思います．

ポイント3. 母集団における統計的な指標が仮にゼロの場合に、手元にあるデータよりも極端な数値が発生する確率を計算する

これまで見てきたのは相関係数の値がゼロの母集団からランダムにデータを取り出したときにサンプルの相関係数がどのような分布をするかということでした。

一方で、実際の実験や調査では、手元のデータの相関係数は計算できるけれど、母集団の相関係数は不明という状況が多く発生します。統計的検定が必要になるのは、このような場合です。

母集団の相関係数が不明な状況で「仮に母集団の相関係数がゼロだとして、手元にあるような相関係数より極端な数値が得られる確率はどれくらいか」を計算するのが相関係数の統計的検定になります。

たとえば，日本の大学生の『外向性』と『1日の発話量』について相関を調べたいと考え，適切な方法で10人の大学生のデータを取得して相関係数を計算したら結果が0.3だったとします．この結果を統計的に検定するということは，通常『仮に母集団（日本の大学生全体）では相関係数がゼロだとして，そこから10人のデータを何回も繰り返し抽出して相関係数を計算したら，0.3より大きい相関係数が得られる確率は5%以下か』を調べていることになります．

先程みたとおり，母集団の相関係数が不明でも、サンプルの人数が決まれば『母集団の相関係数がゼロだと仮定した場合のサンプルの相関係数の分布』を把握することができます。いま、10人のデータから計算した相関係数が0.3だったとすると、母集団の相関係数がゼロのときに、手元のデータでこれより大きな相関係数が得られる確率は、下の図の緑の部分の面積に対応します。

これを計算してみると20%であることがわかります。この20%が有意確率（p）と呼ばれる値で、通常5%以下であれば"帰無仮説が棄却"されるのでした。ここでの帰無仮説とは"手元のデータは相関係数ゼロの母集団から得られた"というもので、これがp=20%だと棄却されない、したがって母集団の相関係数がゼロである可能性が残る＝有意ではないという結果になります。

「あなたの手元にあるデータが、もしも相関係数がゼロの母集団からランダム抽出したデータだとしても、0.3より大きな相関係数が出てくる確率は20%もありますよ」「なるほど、それならこのデータから"母集団に相関がある"と主張するのは難しいですね」という感じでしょうか。

※ここでは説明のために10万回のシュミレーションから作成したサンプルの相関係数の分布を使っていますが、通常は理論的に生成した分布が使われます。

以上、相関係数を例にとって『統計的検定』の考え方のポイントを見てきました。まとめると「仮に母集団の相関係数がゼロだとして、手元にあるような相関係数より極端な数値が得られる確率はどれくらいか」を評価したのが有意確率p値で、この値が5%など一定の基準を下回った場合に帰無仮説を棄却するのが相関係数の統計的検定ということです。

2群間の平均値差のt検定の場合

よく使われる2群間の平均値差のt検定でも考え方は全く同じです。
平均値差がゼロの2つの母集団を想定して、このような母集団から手元にあるデータより大きな平均値差が得られる確率を計算します。この確率が5%以下であれば手元のデータが平均値差ゼロの母集団から得られた可能性は低い＝有意であると考えます。
やはり重要なのは，"差がゼロの母集団から取り出したサンプルについて,差を計算した結果の分布と手元のデータを比較する"という手続きです．

『統計的検定』の基本的な考え方は以上の通りです。有意確率については「母集団の平均値差や相関係数がゼロである確率」、「結果の信頼度をパーセントで表したもの」といった誤った解釈が稀に見られますが、統計的検定の考え方のイメージを把握できれば、結果についても正しい解釈ができるのではないかと思います。この記事が、参考になれば幸いです。