★4/図形 東邦大学医学部医学科2020 問2

問題

　$${AB=5}$$、$${CA=7}$$である$${\triangle ABC}$$において、$${\angle A}$$の二等分線と辺$${BC}$$との交点を$${D}$$、$${\angle B}$$の二等分線と辺$${CA}$$との交点を$${E}$$、線分$${AD}$$と線分$${BE}$$との交点を$${F}$$とする。$${AF:FD=3:1}$$のとき、
$${BD=\dfrac{\fbox{ア}}{\fbox{イ}}}$$であり、$${\dfrac{BF}{EF}=\dfrac{\fbox{ウ}}{\fbox{エ}}}$$である。

解答

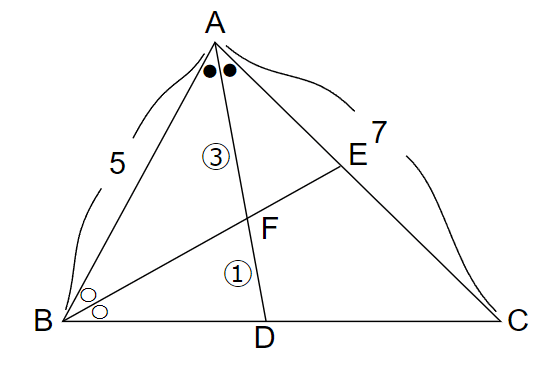
$${AE}$$は$${\angle A}$$の二等分線であるので、$${BD:DC=AB:AC=5:7}$$である。よってメネラウスの定理より

$$
\begin{array}{}
&\dfrac{BC}{BD}×\dfrac{FD}{FA}×\dfrac{AE}{EC}=1\\
\\
\Leftrightarrow &\dfrac{12}{5}×\dfrac{1}{3}×\dfrac{AE}{EC}=1\\
\\
\Leftrightarrow &\dfrac{AE}{EC}=\dfrac{5}{4}\\
\\
&\therefore AE:EC=5:4
\end{array}
$$

同様に$${BE}$$は$${\angle B}$$の二等分線であるので、$${AE:EC=BA:BC}$$である。よって$${5:4=5:BC \therefore BC=4}$$となり、$${BC:BD=12:5}$$より$${BD=\dfrac{5}{3}\cdots(\fbox{ア}～\fbox{イ})}$$
また、メネラウスの定理より

$$
\begin{array}{}
&\dfrac{AC}{EC}×\dfrac{FE}{FB}×\dfrac{BD}{DC}=1\\
\\
\Leftrightarrow &\dfrac{9}{5}×\dfrac{FE}{FB}×\dfrac{5}{7}=1\\
\\
&\therefore \dfrac{BF}{EF}=\dfrac{9}{7}\cdots(\fbox{ウ}～\fbox{エ})\\
\end{array}
$$

総評

　メネラウスの定理と角の二等分線の性質をしっかり使えるかを試す易しい問題です。図形の性質を用いた問題に出くわした時に大事なのが、「ちゃんと教科書レベルのことをすぐ引っ張りだせるか」なので、角の二等分線が設定されていた時などその目印を見逃さないようにしましょう。ちなみに、東邦医学部の数学は問題が多いのでこういった簡単な問題も出ます。