負の二項分布の基礎

負の二項分布とは

「コインを投げた時、5回表が出るまでに裏が何回でるか？」のようなことを考えるとき、この裏が出る回数が従う確率分布を負の二項分布と言います。
※ここの定義はサイトや文献によって変わってくるので要注意。wikipediaでは成功と失敗を逆にして解説がかかれていますが、数理モデルはほぼ同じです。

確率変数$${X}$$が負の二項分布に従う場合、成功確率を$${p}$$(表が出る確率など)として$${r}$$回成功するまでに$${k}$$回失敗する確率は

$$
P(X=k)＝\dbinom{r+k-1}{k}p^r(1-p)^k
$$

と表されます。全体の回数が$${r+k}$$で、$${r+k-1}$$回目までに$${k}$$回失敗して$${r-1}$$回が成功、そして最後の一回が成功になるので、上のような式になります。

また、$${r}$$回成功するのに$${m}$$回試行する確率も負の二項分布と呼ばれ、以下の式で表されます。

$$
P(X=m)=\dbinom{m-1}{r-1}p^r(1-p)^{m-r}
$$

この表し方で$${r=1}$$のとき、負の二項分布は幾何分布と一致します。

負の二項分布の例題

サイコロを投げて$${1}$$が$${5}$$回出るまでに$${1}$$以外の目が$${6}$$回出る確率はいくか。

成功確率は$${p=\dfrac{1}{6}}$$、$${r=5}$$、$${k=6}$$より

$$
\begin{split}
P(X=6)&=\dbinom{r+k-1}{k}p^r(1-p)^k\\
&=\dbinom{10}{6}\Bigl(\dfrac{1}{6}\Bigl)^5\Bigl(\dfrac{5}{6}\Bigl)^6\\
&\simeq9.04×10^{-3}
\end{split}
$$

というわけで約$${0.9%}$$なのでほとんど起こりえないことが分かります。

負の二項分布のグラフ

まずは$${r=3}$$で固定して成功確率$${p}$$を変化させてみます。図は「数学の景色」さんより引用しています。

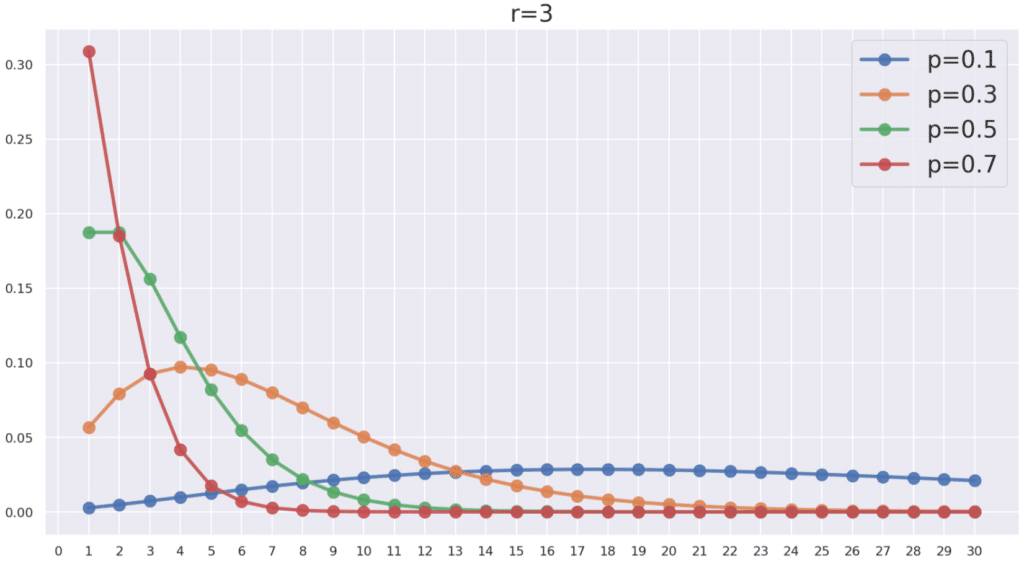
成功確率をあげていくと当然失敗しにくくなるわけで、グラフのピークはどんどん左に寄っていくことが分かります。次は逆に$${p=0.5}$$を固定して$${r}$$を動かします。

$${r}$$の値が小さいとき、言い換えれば成功回数に制限がかかるとき当然失敗できる数も少なくなります。逆に成功回数が大きくなれば失敗できる数も増え、グラフのピークは右に寄ります。

　ゲノム学的には次世代シークエンサーから得られるリードカウントデータの分布が負の二項分布になることが知られており、学ぶ価値は高いと思う。

参考

負の二項分布の定義と例と性質まとめ

負の二項分布 - Wikipedia