色を科学する　その⑨ 色覚の多様性が色彩学の難題を解くカギ＜後編＞

　色覚多様性（いわゆる色覚異常）が色彩学100年にわたる難題であった「ヒトの目の感度」＝錐体分光感度を知るカギになったというお話。＜前編＞のつづきです。

＜前編＞のあらすじ

　前編では、色覚多様性（いわゆる色覚異常）の人が、見分けられない色から、ヒトの錐体の色度座標がわかるというお話をしました。具体的には、見分けられない色を結ぶ、複数の直線が交わる点が、ヒトの錐体の色度座標であり、錐体色度座標がわかれば、錐体分光感度もわかるというものです。そして、見分けられない色、それらを結ぶ直線、直線が交わる点を、それぞれ、混同色、混同色軌跡、混同色中心と呼びます。

色覚多様性の人による等色実験

　なので、混同色をどんどん調べていけばいいのですが、それは大変なので、色覚多様性の人に対し、等色関数を求めたときのような等色実験を行い、そこから数学的に求める手法が取られました。

　余談ですが、この等色実験の被験者を探すのに、新聞広告を出した、という話を聞いたことがあります。色覚検査で使うような仮性同色パタンで「見分けられない人募集！」と。

　色覚多様性の人のうち、2色覚の人はその名の通り、2つの原色ですべての色を等色できます。中でも、R錐体またはG錐体が欠損した1型または2型の方は、Gの光がなくとも、RとBだけですべての単色光を等色できてしまいます。例えば500nmの光もRとBだけでマッチングできるのです。

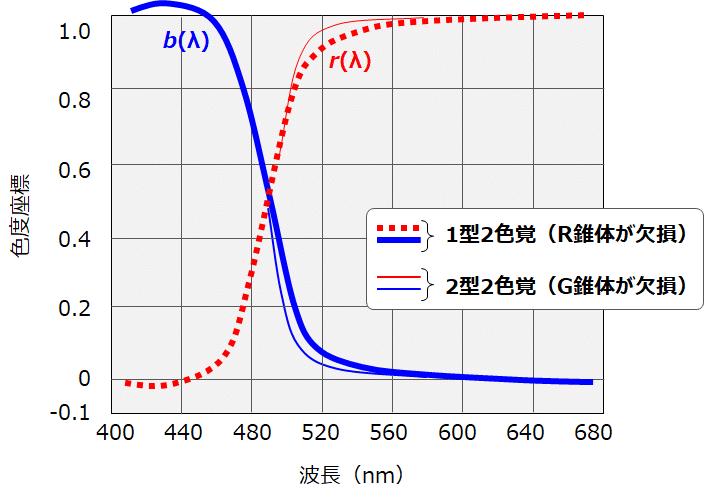
　池田, "色彩工学の基礎", 朝倉書店, (1980) より引用（元はWrightの1946年の書籍より）。縦軸が三刺激値ではなく、色度座標であることに注意。

　そうなると、当然500nmの色度座標が正常色覚の方とは異なり（Gの比率＝gが0になりますから）、その2点が混同色、2点を結ぶ線が混同色軌跡となります。例えば（これは正確な図ではなく、イメージですが）、2型2色覚の場合、500nmの単色光に対する色度座標は点CDになり、正常色覚の500nmの色度C500とを結ぶと混同色軌跡となります。

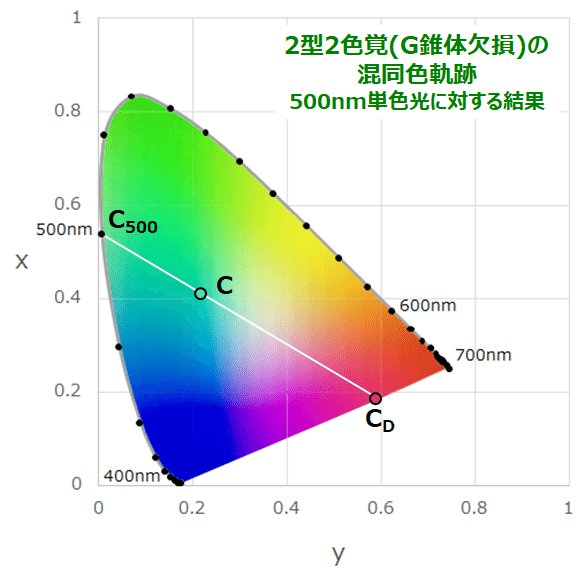
　というのも、、、色度図の性質上、任意の色CはC500とCDを適当な比率で混色すると等色します。それは、2型2色覚の人でも成立し、なおかつ、CはC500とCDも等色しているので、C500とCDを結ぶ直線状は、すべて同じ色に見える＝混同色軌跡となるためです。

混同色軌跡が1点に交わり…

　このようにして、1型、2型、3型2色覚のそれぞれに対し、求めた混同色軌跡を何本も引くと、ある一点に収斂し、そこが混同色中心＝R、G、Bの錐体座標となるのです（実際にはRGB表色系で複雑な補正を行ってからXYZ表色系に変換する）。ちなみに、3型（B錐体の欠損）は非常にレアケースでデータ自体が少ないです。

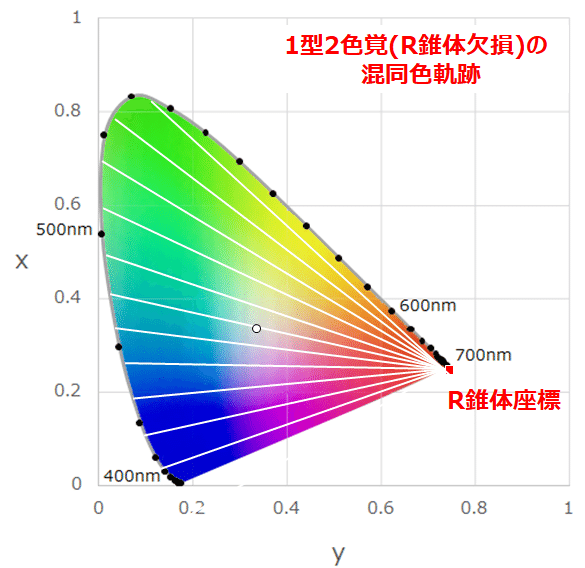
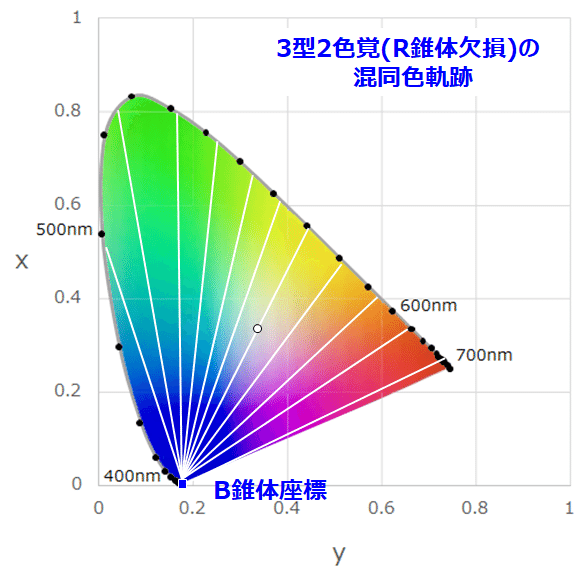
　G錐体はかなり外れたところにあり、おもいっきり「虚色」ですね。これは後ほど…

　ここで、白い〇は白色点です。なので、ここを通る線上はすべて白色（無彩色）に見えます、それが鮮やかな単色光でもです。

　そして、1型および2型2色覚では、この白色点を通るラインより短波長側は、色相としては青と区別がつかず、長波長側は同様に黄色と区別がつかないのです。（他人がどう見えているか？はどうやってもわからないので、青または黄色に見ているとは言いきれない）。3型2色覚では、同様に短波長側は緑、長波長側は赤と区別がつかないのです。

　これは、片眼が正常色覚、もう片眼が1型および2型2色覚という稀な人の等色実験によりわかっています。500nmより短波長の単色光はすべて475nmの青い単色光と同じ色に見え、長波長の単色光はすべて、575nmの黄色い単色光と同じ色に見えるという結果が出ています。

とうとうRGB錐体分光感度へ！　が、しかし…

　混同色軌跡が収斂する混同色中心の座標として得られたRGB各錐体座標をもとに＜前編＞で紹介した方法で3x3変換行列を求め、変換した結果が下記です（この時、XYZ表色系の等色関数はジャッド修正後のものを使います）。

※錐体色度座標はSmith & Pokornyによる

ここで気になることが、、、

①G錐体とR錐体の感度が非常に似ており、そのピークの差は30nmくらいしかない

②R錐体の感度ピークは570nm、感度の幅も広いので、「赤」と言えるのか？（G錐体も感度の幅が広い）

　①に関しては、以前も書きましたが、もともと同じものが分化したという経緯によります。2色覚において1型と2型（RまたはG錐体の欠損）が多いことや、1型と2型が同じ動きをする（↑で書いた等色実験結果や色相の識別など）のもそのためです（逆にいうとB錐体が常に単独行動）。

　赤と緑の識別はこのRおよびG錐体の応答の差で行います。なので、どちらかが欠損すると識別ができなくなり、黄色と混同してしまいます。あくまでイメージですが、Bの応答が十分に小さい状態で、G>Rなら緑、G<Rなら赤、G=Rなら黄といったような。

　②に関しては、「赤、青、緑に感度を持つ3つの視細胞がある」と100年間信じてきたのに、実際には、青、緑～黄、緑～赤に感度を持っていたことが、分光感度を求めて初めて分かりました。そこで、専門的にはR、G、B錐体とは呼ばず、「L、M、S錐体」と呼びます。LはLong-Wavelength（長波長に感度を持つ）、MはMiddle-Wavelength（中波長）、SはShort-Wavelength（短波長）の略です。

3次元で考えよう

　G(M)錐体の座標が他とくらべ外れたところにあり、緑のはずなのに赤に近い座標にある（虚色なので近いことに意味ないですが）のは、すごく気持ち悪いです。

　これは、2次元の色度図で考えているからで、3次元の色空間にすると原因が見えてきます。錐体色度座標は各錐体の色ベクトルがXYZ色空間の単位面と交差する点なので、その様子を描くと下記のようになります。

　R(L)とB(S)錐体のベクトルは、それぞれ、XとZに近いのですが、G(M)錐体のベクトル（軸）だけは、XYZ空間から見ると、"あさっての方向"を向いていています。なので、XYZの単位面との交点が"あの位置"になってしまうのです。

　3次元で考えると色々見えてくるのは、混同色軌跡も同じです。＜前編＞で紹介した2次元の色度図で表現した混同色軌跡を3次元で考えてみます。

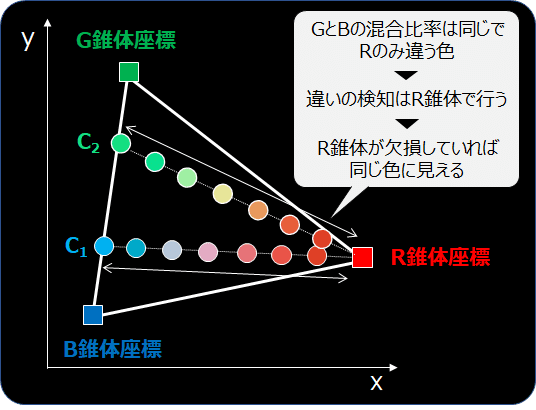
下図で、C1はBとG錐体だけで表現でき、そこにR錐体の成分をどんどん足していくと、最終背的にR錐体のベクトルと同じになります。しかし、R錐体の成分しか差がないので、これら一連の色はR錐体が欠損している人には見わけが付けられません。

　C1とBとG錐体の比率が違うだけのC2でも同じことが言え、R錐体の成分をどんどん足していくと、C1の場合と同じR錐体のベクトルへ収斂していきます。

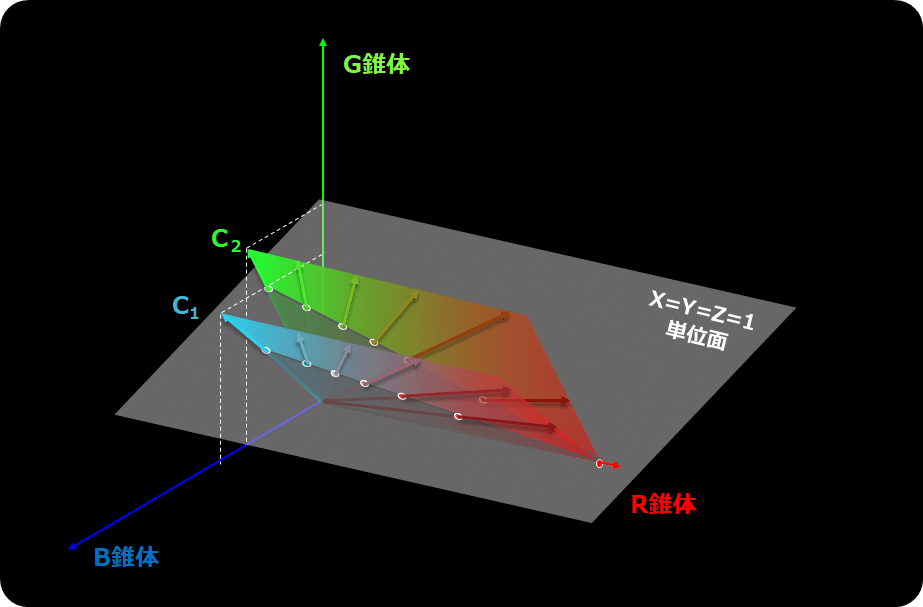
　これらの色ベクトルが単位面と交差する点が、xy色度図上の混同色軌跡なのです。ベクトルで考えると見方が変わりますね！

　以上、＜前編＞＜後編＞含め終了！長かった、、、