
5分で分かる深層学習
深層学習を数学好きの人のためにできるだけ抽象的に解説します。
犬と猫を見分ける問題
画像が犬か猫を見分ける問題を考えます。深層学習(機械学習一般)では、まず訓練データを用意します。訓練データとは、犬か猫の画像のサンプルとそれが犬か猫であるかを示すラベルからなります。画像は大きな次元の数値ベクトルx_i, i = 1, ..., nで表せます。それに犬ならばy_i=1, 猫ならばy_i=0という値が割り振られています。この時、次のようになる関数Fを

を求めるたいです。もちろん、このようなFはどんなものでもあり得ます。与えられたx_i以外はすべて猫と判定するFもあり得ます。これでは意味がないので「自然な」Fを考えます。つまりある自然な関数fで

と書けると仮定します。ここでθはパラメータのベクトルです。深層学習ではfは一定の構造を持つニューラルネットワークで表されています。ニューラルネットや深層学習で使われるニューラルネットの構造についてはQiitaなどにたくさん記事があるのでそちらを参考にしてください。
深層学習は、猫と犬を見分ける問題を学習データを最もよく説明するθを見つける問題にします。
ロス関数
深層学習を用いるとf(θ, x)は連続関数でθについて微分可能になります。fの値は必ずしも0, 1とは限りませんが、普通シグモイド関数

と合成して(0, 1)区間の関数にして、確率と解釈します。なのでf(θ, x)の値はxが犬の画像である「確率」です。学習データがf(θ, x)の元で生成される確率は

です。これをθについて最大化します。色々な事情から対数のマイナスをとって

と定義します。これをロス関数といいます。問題はロス関数を最小化することになりました。
確率的勾配降下法
深層学習の場合、fの形が複雑なので最適化を解析的に行うことはできません。そこで確率的勾配降下法を用います。まず訓練データから(できればランダムに)b個のサンプルを取ってきいます。bをバッチサイズと呼びます。その上でこのサンプルを使ってLossを計算し、
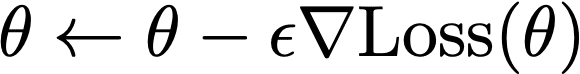
とθを更新します。εは小さな数です。つぎにまた新たなb個のサンプルを取ってきて...と繰り返します。これによりθがLoss(θ)が小さいところに近づいていくことを期待します。全訓練データではなくサンプリングされた訓練データを使うのはθに揺らぎを与えて局所最適解に落ち込まないようにするためです。
実際には収束を早めるためさらに複雑な方法が用いられます。εを動的に変化させたり、慣性を入れたりします。Adamという手法がよく使われています。
どの時点でθの更新を止めるべきかは難しい問題です。訓練データの一部を別に取り分けておいて、それをつかって性能を計測して改善があまり見られなくなった時点で打ち切ることが実際はよく行われています。
θが決まれば、あとはf(θ, x)>0.5となれば犬と判定し、<ならば猫と判定します。
まとめ
簡単に深層学習が基づく原理について説明しました。深層学習といっていますが、ニューラルネットの構造の説明は何もしていません。問題ごとにさまざまな構造が提案されています。 Qiitaとかにたくさん記事があると思います。
この記事が気に入ったらサポートをしてみませんか?
