
「学力対数の法則」の検証
イブリースさんが私の記事を引用してくれました。その記事を読むと、後半に「学力対数の法則」というのものが打ち出されています。「学力対数の法則」はこのように定義されています。
学力対数の法則とは「学歴の存在比がN倍の場合、同レベルの学力の持ち主の存在比は1/Nに低下する」というものである。
具体的には、イブリースさんは次のような学力レベルを定義した上で、レベル間の存在比はN=3.3倍(2レベル違うと10倍)となると論じています。
レベル7 東大理三
レベル6 阪大医 慶応医
レベル5 東大 地方旧帝医 首都圏医
レベル4 一橋 東工大 地方国立医
レベル3 早慶 旧帝
レベル2 MARCH 関関同立 地方国立
レベル1 日東駒専 地方私立大
レベル0 その他
この学力レベルは、別のWebサイトが整理している学歴ランクともほぼ一致します。Lv 7・6=宇宙、Lv5=S級上位、Lv4=S級中下位、Lv3=A級、Lv2=B級という対比です。それぞれの筆者が定義したレベル分け/ランク分けがほぼ一致するということは、世の中一般でも、これくらいの段階で学歴の差がイメージされているのだろうと思います。
じゃあ、レベル分け/ランク分けがなんとなく妥当だとして、本当に存在比(人数)が対数になっているのか検証してみよう、ということで、簡単な分析をやってみました。
駿台全国模試の判定偏差値の設定基準を私が勘違いしていたことがわかりました。現在、過去の分析を再分析中です。以下の記事内容は今後修正の予定です。修正前の記事としてご覧下さい。(2024.10.12)
0. まとめ
駿台全国模試、全統記述模試、共通テストリサーチを用いて検証した結果、イブリースさんの「学力対数の法則」は成立していると言える。
ただし、対数の底数は2レベル差で1/10(1レベル差で1/3.3)ではなく、2レベル差で1/8倍(1レベル差で1/2.8)が実態に近い数字と考えられる。
1. 比較の基準合わせ
今回は複数の学力レベル間の比較を行うのですが、単純に模試の偏差値などを用いる場合、国立と私立、入試の科目数、文系と理系などの特性の違いが影響してしまいます。そこで、最初に基準合わせが必要となります。
そこで、今回の分析に辺り、次の3つの補正を行います。駿台全国模試をサンプルに説明します。法学部/工学系(電気電子系)/医学部医学科の3つの区分で、学力レベルの異なる大学をいくつか抽出したのが次の表です。なお、手持ちデータを組み合わせているため、項目ごとに引用/集計元のデータの年月が異なります。ただ、大きな違いはないと思われるので、気にせずに分析しています。

左から6列目のブルーの数字が、駿台全国模試のB判定偏差値(2023年7月調査)です。例えば、東北大は法学部も工学部も偏差値57となっています。ただ、入試科目は法学部が3科目(国数英)、工学部は4科目(数英+理科2)と勉強の負荷は理系の方が大きいはずです。
また、明治大学は法学部は偏差値56と東北大とほぼ同等なのに対し、理工学部は偏差値52と大きく開きがあります。そして科目数は明治大の理工は3科目であり、東北大・工学部よりも勉強の負荷は低いです(さらに東北大はセンターもある)。
さらに、共通テストリサーチや駿台の追跡調査などを見ると、文系と理系の母集団は学力が違い、文系の偏差値は理系の偏差値よりも高くでるようです。私のこれまでの分析を見ると、文系偏差値=理系偏差値+2くらいのようです。
駿台模試のB判定偏差値には、こうした違いが反映されていません。さらに、実際の合格者平均偏差値はB判定偏差値よりも下にあるようですし、私立大は併願合格者が抜けるため、入学者平均偏差値は更に下になるようです。
つまり、駿台模試のB判定偏差値の数字を、学力レベル間の比較指標として、そのまま使用することはできません。そのため、この補正を次の3段階で実施しています。
①科目数と文系・理系の差の補正
科目数は1科目の増減で偏差値1を調整します。また、文系と理系の基準合わせのために、文系はマイナス1、理系はプラス1しています。この補正後のボーダー偏差値が緑色の列の「補正偏差値①」です。この数字は同一基準(4教科5科目•同じ学力の母集団)での、合格率60%の難易度です。
基準を合わせたことで、大学間で学部構成の違いがあっても、この数字定員比の加重平均を取ることで大学同士の合格難易度の比較ができるようになります。世間一般の合格難易度に近いのがこの数字(補正偏差値①)と言えます。
②合格者平均との差の補正
過去に模試判定モデルを作成した時に考察した通り、同じボーダー偏差値でも受験者倍率によって、合格者の分布は変わるはずです。高私立文系のように倍率の学部•学科はD判定のチャレンジ受験生が多くなります。この時、模試判定の合格可能性が正しなら、合格者の分布はボーダー(B判定)より下に膨らみます。結果、高倍率の学部•学科の合格者平均偏差値はボーダー偏差値よりかなり低いところに位置することになります。
この考え方の下で、駿台模試の追跡データと過去の分析での推定データを用いてマイナス幅を推定し、国立文系はマイナス1、国立理系はマイナス3、国立医医はマイナス4、私立は一律でマイナス3しています。この補正後が黄色の列の「補正偏差値②」で、合格者平均偏差値の近似値となります。
③入学者平均との差の補正
私立大では上位の大学に合格した併願合格者が辞退し、チャレンジ受験の合格者はそのまま入学すると考えられます。この場合、合格者分布の上位が抜けて、下位は残るので、入学者分布は下に歪みます。その結果、入学者平均偏差値は合格者平均偏差値より一段下がることになります。一方、国立大は本命受験が大半なので、合格者分布と入学者分布はほぼ同じはずです。
この考え方の下で、過去の分析での推定データから、私立は一律でマイナス2しています。この補正後の数字がオレンジ色の列の「補正偏差値③」で、入学者平均偏差値の近似値となります。
この3つの補正を行うと、4教科5科目(東大と同じ)で入試を行った場合の、大学入学者の学力を比較することになります。私立大は3つの補正が重なるので、補正偏差値③(入学者平均)は駿台B判定偏差値よりも大きく下がります。
例えば、東北大・法学部の駿台B判定は57ですが、補正偏差値③(入学者平均)は53に下がります。一方、明治大・法学部の駿台B判定は56なのが、補正偏差値③(入学者平均)は48に下がります。東北大・法学部と明治大・法学部は、駿台B判定偏差値ではほぼ同じ水準だったのが、入学者平均では偏差値5の格差=1ランク違いとなります。補正偏差値③(入学者平均)の方が、多くの方の感覚的な大学ランクのイメージに近いのではないかと思います。
2. 駿台全国模試での検証
上記の補正を大学・学部・学科・入試方式ごとに実施し、大学ごとに定員の加重平均を取って、それぞれの偏差値数字を算出したのがこの表です。なお、データが上手く揃わないケースがあり、いくつかの大学では一部データ欠損した上での集計となっています。ただ、大半は集計しており、さらに学力レベルごとに定員比加重平均で集計するため、一部のデータ欠損は今回の検証に対して大きな影響はないと考えます。

駿台B判定、補正偏差値①の列を見ると、レベルが1つ下がると、偏差値が5〜7くらい下がることが見て取れます。このギャップは補正偏差値②③でも、レベル4以上は変わりません。一方、私立大学が入るレベル3以下では、ギャップが拡大します。
この偏差値ギャップが順位=人数にどれくらい影響を与えるかを分析しているのが右半分です。駿台全国模試の受験者は3万人として試算しています。
例えば、60%判定(4教科5科目基準)の列を見ると、レベル7の東大理三や京大医医でB判定を取るには48位以内に入る必要があることがわかります。その下を見ていくと、レベル6の医医なら309位以内、レベル5の東大なら1,251位以内に入ればよく、レベル2のMARCHなら16,317位以内と過半数には入れば十分となります。
この順位=人数が1レベル差で何倍になるかを計算したのが、右端です。60%判定(4教科5科目基準)は、Lv7/Lv6が6.4倍、Lv6/Lv5が4.1倍で、Lv3/Lv2が2.1倍となります。この幾何平均を取ると、黄色のセルの3.2倍です。合格者平均、入学者平均も同様の計算を行い、3つの幾何平均の平均を取ると、オレンジ色のセルの2.8倍となります。
この2.8倍というのは、学力レベルが1つ上がると、平均的には人数が1/2.8になることを意味します。2.8×2.8=8.0であることから、2レベルの差は1/8となります。
この人数の動きをグラフにしたのがこちらになります。

「学力対数の法則」がよりわかるように、縦軸を対数目盛にするとこうなります。
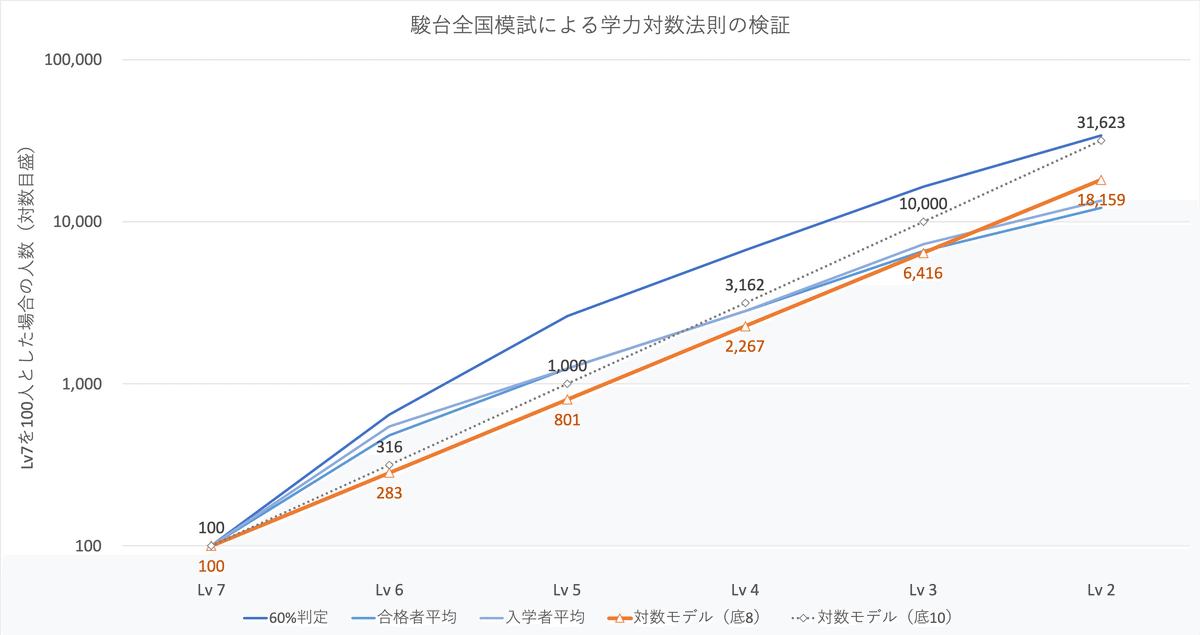
青の3本のグラフが分析データ、オレンジが3つの平均、グレーの点が2レベル差で1/10(底10)のイブリースさんのモデルです。一番上の濃い青が合格60%の難易度差のイメージで、これは概ねイブリースさんのモデルに近いです。一方、合格者平均や入学者平均はそこまで急激には伸びず、薄いブルーの2本は下側にあります。平均するとオレンジのグラフの底8となります。
Lv 2のMARCHが偏差値50の前後にあることから、受験者が正規分布する前提だと偏差値50を割ると人数の増幅が小さくなります。そのため、対数目盛のグラフでは、ブルーの折れ線は右端のLv3→Lv2で傾きがなだからになってしまうようです。
3. その他の検証
駿台全国模試以外の検証として、全統記述模試(河合塾)と共通テストリサーチでも同様の分析を行ってみました。Lv3の早慶とLv2のMARCHは、共通テスト受験が限定的なので、共通テストリサーチの分析では除外しています。

1レベル差の倍率=底数は、駿台全国模試が2.8倍だったのに対して、全統記述模試も共通テストリサーチも1/1.8前後の小さな値となりました。Lv 4/Lv 3はどの数字も近い数字(1/2.0〜1/2.6)、全統記述模試のLv 3/Lv 2は失速しておらず、Lv3以下はどの比較でも大差ないのかもしれません。
一方、学力最上位のLv7〜4となると、全統記述模試や共通テストリサーチは学力差が偏差値の差に出にくくなると考えられます。受験者が多い右に行けば行くほど、倍率が小さくなっています。
上記のようなバラツキがある中で、今回は高レベル側の分析がメインなので、駿台全国模試からの算出値を採用することにします。この場合、1レベル差の倍率は1/2.8となります。
4. 最後に
上記の通り、イブリースさんの「学力対数の法則」は成立することが検証できました。一方、底は2レベル差で1/10倍(1レベル差1/3.3)より小さく、2レベル差で1/8倍(1レベル差1/2.8)というのが計算結果で、少し差がでました。とはいえ、Lv 3/Lv 2が低めに出ていると考えられるため、もう少し高い数字で1レベル差で1/3と見てもよいのかもしれません。
この算出がどこまで正確性があるかは全くわからないこともあり、メッセージのわかりやすさも考えると、「学力対数の法則は成立し、同じ学力レベルの人数は、1レベル下がると1/3に、2レベル上がると1/10となる」と言ってしまってよいと思います。
この記事が気に入ったらサポートをしてみませんか?
