
【数理的溢れ話19パス目】日常生活でも役立つ「陰謀論の予防にもなるかもしれない」サイズ感覚の洗練について。
とりあえず次のステップに進む為のメモがてら。これまでの投稿のまとめの様なもの。
泡沫事象(Foamy Event)
そもそも、まずは般若心経における「色即是空空即是色」の文言や量子力学における「シュレディンガーの猫」の例えにある様な曖昧な状態を乗り越えてある事象が「観測出来た」と確信するに至るプロセスを固めないといけません。
シュレーディンガーの猫は、量子力学の奇妙さを説明するために物理学者エルヴィン・シュレーディンガーが提唱した思考実験です。この実験では、次のような状況が設定されています。
密閉された箱の中に猫を入れ、放射性物質、ガイガーカウンター、毒ガス、ハンマーを配置する。
放射性物質が崩壊すると、ガイガーカウンターがそれを検出し、ハンマーが作動して毒ガスが放出され、猫が死亡する。
放射性物質の崩壊は量子力学的に確率的な事象であり、観測されるまで崩壊しているかどうかは不確定な状態にある。
この状況下では、観測されるまで猫は「生きている状態」と「死んでいる状態」が重なった「重ね合わせ状態」にあるとされ、観測が行われた瞬間にどちらかの状態が決まる、というのがシュレーディンガーの主張です。この思考実験は、量子力学の「観測問題」や、ミクロとマクロの世界をどう結びつけるかという議論に使われています。
数学的背景
数学ではここで「全体に対して十分小さい区間」なる概念が登場し、それ以下だと「存在しても存在しなくても同じ」と考えて切り捨ててしまいます。それにつけても「全体に対して十分小さい区間」とは?要するにネイピア数e(2.718282…)の事です。幾らでも小さな桁が考えられる加減算では「加法単位元0に極限まで近い最小の増減量」が無限に考えられてしまうので収束の気配も見せませんが、剰余算では「乗法単位元1に極限まで近い最小の増減量」がこの辺りで収束するのでその発見以降の数学にとって重要な基準となりました。
$$
e^{+1}=\lim_{n→∞}(1+\frac{1}{n})^n=2.718282…
$$
$$
e^{-1}=\lim_{n→∞}(1-\frac{1}{n})^n=\frac{1}{e}=0.3678794…
$$
ところで以下の投稿では二項分布(Binomial Distribution)$${B(x;n,p)={}_nC_xp^x(1-p)^{n-x}}$$(p=成功率、n=試行回数の場合のx回成功率)で期待値pが$${p=1-p=\frac{1}{2}}$$と均等割になる場合について掘り下げましたが、ここでは真逆にpと1-pの差が最大に近付く場合、すなわちどちらか片方が「全体に対して十分小さい区間」以下となる場合について考えなくてはいけません。
分布の種類がポワソン分布(Poisson Distribution)$${PO(x;λ)=\frac{λ^xe^{-λ}}{x!}}$$に推移します。これは「観測単位において平均発回数λの場合のx回発生率」の分布で期待値(平均)E(X)も分散V(X)=$${σ^2}$$パラメーターのλそのもの。

正規分布と仮定した場合の分散区間(次第に1匹未満の目撃例がレアケースとなっていく)。概ねλ=7の時の-2σ以上の出現率が5%水準の有意味度=$${\frac{1}{60}=0.01666…}$$を下回る泡沫事象に分類される展開に。

λ=1(0<x<2)の時、
$$
1σ_{min}=1-\sqrt{1}=1-1=0,{1σ_{max}=1+\sqrt{1}=1+1=2}
$$
λ=2(0<x<4)の時、
$$
1σ_{min}=2-\sqrt{2}=0.5857864…,1σ_{max}=2+\sqrt{2}=3.414214…
$$
λ=3(0<x<6)の時、
$$
1σ_{min}=3-\sqrt{3}=1.267949…,1σ_{max}=3+\sqrt{3}=4.732051…
$$
λ=4(0<x<8)の時、
$$
1σ_{min}=4-\sqrt{4}=2,1σ_{max}=4+\sqrt{4}=6
$$
$$
2σ_{min}=4-2\sqrt{4}=0,2σ_{max}=4+2\sqrt{4}=8
$$
λ=5(0<x<10)の時、
$$
1σ_{min}=5-\sqrt{5}=2.763932…,1σ_{max}=5+\sqrt{5}=7.236068…
$$
$$
2σ_{min}=5-2\sqrt{5}=0.527864…,2σ_{max}=5+2\sqrt{5}=9.472136…
$$
λ=6(0<x<12)の時、
$$
1σ_{min}=6-\sqrt{6}=3.55051…,1σ_{max}=6+\sqrt{6}=8.44949…
$$
$$
2σ_{min}=6-2\sqrt{6}=1.101021…,2σ_{max}=6+2\sqrt{6}=10.89898…
$$
λ=7(0<x<14)の時、
$$
1σ_{min}=7-\sqrt{7}=4.354249…,1σ_{max}=7+\sqrt{7}=9.645751…
$$
$$
2σ_{min}=7-2\sqrt{7}=1.708497…,2σ_{max}=7+2\sqrt{7}=12.2915…
$$

ただし二項分布の場合同様、条件によって正規分布N(x;λ,λ)での近似が可能となるのはλ=5~10くらいから。
期待値(平均)E(X)=λ…xが整数の場合に注目すると、その最頻値はxがλ-1)の箇所とλの場合に現れ、そこだけ勾配が平坦となる。そして両者の差はλが大きくなるほど小さくなり、究極的には$${x=λ}$$に収束。
$$
\lim_{λ→∞}(λ-1)λ=λ^2
$$

分散V(X)=λ…とりあえず平均値λの二倍を「実元(Reaal Element)」と考えた時、それを越えた範囲にある「虚元(Lmaginal Element)」の範囲がλ=7以降、出現確率が5%水準の有緑=$${\frac{1}{60}=0.01666…}$$を下回る泡沫事象となる。なおその時点でベルカーブ分布上の最頻値以の割合は0.45前後、それより上の割合は0.53%程度。つまり完全に左右対称ではないが、中央極限定理に従って分布が中央に寄るので、それでも十分な精度?

さらに数式から読み取れる特徴を追求するなら…
$$
PO(x;λ)=\frac{λ^xe^{-λ}}{x!}=e^{-λ}*\frac{λ^x}{x!}
$$
左項$${e^{-λ}}$$は「観測単位において1回も観測されない確率が$${e^{-λ}}$$回」である事を意味する。λ=5の時に$${e^{-5}=0.006737947…}$$となって出現確率が5%水準の有意味水準=$${\frac{1}{60}=0.01666…}$$を下回る泡沫事象となる(正規分布N(x;λ,λ)での近似が可能となる条件と重なる)。
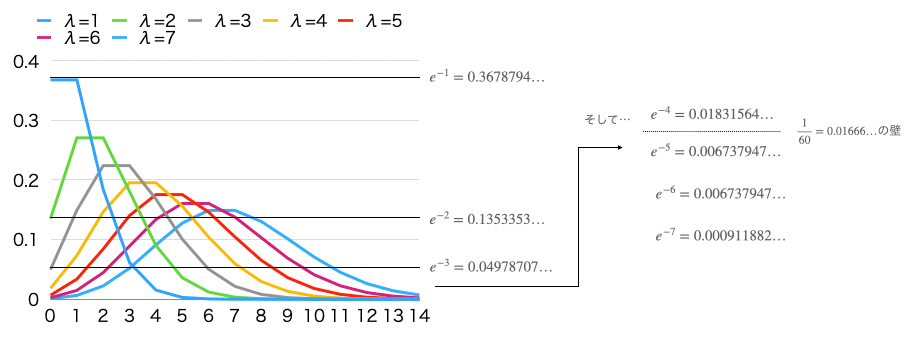
右項$${\frac{λ^x}{x!}}$$は指数関数$${e^{+λ}}$$のテイラー級数$${\sum_{x=1}^∞\frac{λ^x}{x!}}$$の一部であり、これと左項${e^{-λ}}$$を掛け合わせた結果が1となる(ポアソン分布が確率分布である証明)。
ただしテイラー級数はあくまで近似式に過ぎず、無限に計算は続けられないのでどうしても実元(Real Element)に対する虚元(Imaginal Element)つまり「その他」概念の導入を避けられなかったりします。

ところでフランスの数学者ポアソン(Siméon Denis Poisson、1781年~1840年)が1838年に発表したポワソン分布が実用上重要になったのは1907年の金融危機が契機となったとされています。
一つ目の危機が起きたのは一九〇七年のことだった。この年の金融危機でアメリカ電話電信会社(AT&T)が所有するベル電話システムの存続が危うくなったのだ。アレクサンダー・グラハム・ベルの特許は数年前に切れ、会社自体も拡大しすぎていた。ベルが破綻を回避できたのは、一にも二にもモルガン社の主導によって銀行協会が介入したおかげだった。
このとき、監督官庁はベル社が地方の競争相手より安く優れたサービスを提供できるという証拠を示すよう求めた。あいにくベルの電話回線は、昼前後に負荷が過剰になることが多かった。あまりに多くの利用者が、この時間帯に電話をかけようとしたのだ。残りの時間帯──一日の八割──の処理能力にはまだまだ余裕があったのだが、AT&Tに限らずどの会社にも、ピーク時に予想されるすべての電話を処理できるだけのシステムを構築する力はなかった。
この時台頭したのがニューヨーク出身の米国人エンジニアエドワード・C・モリーナ(Edward Charles Dixon Molina,1877年~1964)でした。
当時、AT&Tのベル電話システムは、問題解決に新たな数学的アプローチを取り入れようとしていた。モリーナの上司であるジョージ・アシュレイ・キャンベルは、フランスでポアンカレとともに確率を研究したことがあったが、それ以外の従業員は、『エンサイクロペディア・ブリタニカ』で確率を学んでいた。モリーナは数学と物理学を独力で学び、やがてアメリカ国内におけるベイズやラプラスの確率論の第一人者となった。
最終的にはベイズの定理を用いたトランザクション処理装置を完成させて技術史にその名を残しましたが、その過程でポワソン分布が「再発見」されたという次第。
(モリーナは)ポアソン分布を独力で発見し、すぐにモリーナ分布と命名したところが、ラプラスの弟子のシメオン・ドニ・ポアソンがまったく同じ分布に関する論文を書いていたことを知り、恥ずかしい思いをすることとなった。
なおポアソン分布でλ=1の場合、すなわち「全体に対して十分小さい区間に事象が1回観測されるかされないか程度の確率」は「その事象が1回発生する単位区間」と考えられ、これを「観測単位において平均発生率λ回の現象が、観測期間xに観測される間隔」という方向に発展させたのが「ポワソン分布の逆関数」指数分布(Exponential Distribution)X ∼ Exp (x:λ)=$${λe^{λx}}$$となります。平均$E(X)=\frac{1}{λ}$、分散$V(X)=λ^2$。

各パラメーターの動きに注目すると、まず平均観察期間λ=1の時にその事象が1回も観察されない(x=0)確率が$${e^{-1}=\frac{1}{e}=0.3678794…}$$となり、以降は観察期間xを増やす都度$${\frac{1}{e^{-x+1}}}$$で推移し、x=4以上の時に5%水準の有意味度=$${\frac{1}{60}=0.01666…}$$を下回る泡沫事象となる。なおこの分布展開は「平均観察期間λ=1時点での生存率が$${e^{-1}=\frac{1}{e}=0.3678794…}$$の観察対象が観察期間を増やしたλ=x段階それぞれでの生存率」とも解釈可能で、だから「生存曲線」とも呼ばれ、それはまさに機械の故障率を扱うワイブル分布(Weibull distribution,1939年にスウェーデンの数学者ワイブル(Ernst Hjalmar Waloddi Weibull, 1887年~1979年)が発見)のバスタブ曲線における「偶発故障域(Random Failure Area)」に該当する(分布を「生存率」でなく「死亡率」に割り当てている点に注意)。

一方、パラメーターλを増やす事は観察単位をその数で割るのと同義。概ねx=6以上の時に5%水準の有意味度=$${\frac{1}{60}=0.01666…}$$を下回る泡沫事象となる。
まさしく以下の数学史区分における「統計学者と母集団推定の時代」において産業革命浸透を契機に「大数学者」の存続が経済構造上不可能となる一方、技術の最先端で「叩き上げの技術者」が台頭してきた景色そのものという次第…
数秘術師や魔術師の時代(イタリア・ルネサンス期~近世)
大数学者や大物理学者の時代(大航海時代~1848年革命の頃)
統計学者と母集団推定の時代(産業革命時代~現代)
機械学習と意味分布論の時代(第二次世界大戦期~現在)
直感的理解
とまぁ理屈はこうなってる訳ですが、実用にあたっては「この考え方に従うと大体どれぐらい全体サイズに対して小さいと切り捨て対象になるのか」さえ理解してれば十分でしょう。
60進法に換算すると1時間(60分)に対する1分未満、1分(60秒)に対する1秒未満。空間距離でいうと地球全体に対して「丸いと感じられなくなる」境界線が大体「人間が1日以内に往復可能で、かつ訪問先で有意味な時間が過ごせる範囲(サラリーマンでいうと通勤可能圏)」という感じ。
スズメバチなどを数える時の様に、十分長い観測期間(例えば1週間)における観測数が2回未満なら「たまたま目撃されたに過ぎない(あるいは単なる見間違い)」可能性を疑う。
要するに「社会全体に対して個人はちっぽけな存在に過ぎない」と嘆く場合における「個人」のサイズで、社会の構成要素はそれより小さくはなり得ないとかそういう感じ話で、それは何よりもまず「虚元(Imaginal Element)」領域に観測不可能な形で潜在するというイメージ。
統計学的事象(Statistical Event)
科学的実証主義の立場に立つと観測対象が確実に実在するという確信は、その分布(Distribution)の具合を確かめる過程で次第に高まっていきます。
科学的実証主義は、知識は経験や観察、実験によって得られるものであり、検証可能なものだけが真理として認められるという立場です。この哲学的立場は、19世紀の哲学者オーギュスト・コントによって提唱され、その後、論理実証主義の形で20世紀に影響を与えました。
科学的実証主義の基本的な考え方
経験に基づく知識:
すべての知識は観察や経験、実験を通じて得られるものであるとされ、理論的な推論や形而上学的な主張(経験的に確認できないもの)は、科学的な知識として認められません。経験的証拠に基づいて初めて主張が成立します。
検証可能性:
科学的命題は、その命題が観察や実験によって検証されるかどうかにかかっています。つまり、検証可能でない命題(例えば、神や霊魂の存在についての議論)は、科学の範疇には含まれないという考えです。
理論と観察の関係:
理論は観察によって支持されるべきであり、科学的理論は観察と実験を通じて繰り返し確認される必要があります。理論的な構造はあっても、最終的には観察やデータによって裏付けられることが求められます。
形而上学への拒絶:
科学的実証主義では、形而上学的な議論や、経験的に確認できない概念は拒否されます。例えば、魂や神、宇宙の究極の目的といった概念は、実証的に証明できないため、科学的な議論としては扱われません。
科学的実証主義の限界
観察の限界:
経験や観察に基づく知識は、観察装置や人間の感覚の制約に依存するため、必ずしも完全な真実を反映しているとは限りません。また、観察の結果が理論に依存してしまうこともあります。
理論の進展:
科学的理論は時として観察データと矛盾することがありますが、それでも理論が支持されることがあります。例えば、アインシュタインの相対性理論は、その当時の観察結果とは必ずしも一致していませんでしたが、理論的に支持されていました。このようなケースでは、実証主義だけでは科学の進展を説明しきれないことがあります。
検証可能性の問題: 論理的に検証可能かどうかの判断が困難な理論も存在します。量子力学や宇宙論のような分野では、直接的な観察が難しい事象に対する理論が提唱されており、これらは従来の実証主義の枠組みでは取り扱いが難しい場合があります。
結論
科学的実証主義は、科学の基盤として観察や経験を重視し、検証可能なものだけを知識として受け入れる立場です。しかし、科学の進展とともに、その限界も指摘されており、より広範な哲学的視点(例:科学的現実主義や構成主義など)との対話が求められることが増えてきています。
逆をいえば「分布」が観測される様になったらとりあえず「何かがある状態a=実元」のみで被覆された空間を前提に考えられる様になるので「何もない状態b=虚元」については忘れていいと考えるのが科学実証主義の流儀となる訳です。
「観測数0」の場合…$${(a+b)^0=1}$$の状態。「ある(実元a)」と「ない(虚元b)」の峻別が本当に不可能。
「観測数1」の場合…$${(a+b)^1=a+b}$$の状態。とりあえずベイズ統計学における「理由不十分の原則(principle of insufficient reason).」に従って「ある(実元a)」=$${\frac{1}{2}=0.5}$$、「ない(純虚元$${b^1}$$)」=$${\frac{1}{2}=0.5}$$と割り当てる。
「観測数2」の場合…「ある(実元a)」=$${\frac{3}{4}=0.75}$$、「ない(純虚元$${b^2}$$)」=$${\frac{1}{4}=0.25}$$

「観測数3」の場合…「ある(実元a)」=$${\frac{7}{8}=0.875}$$、「ない(純虚元$${b^3}$$)」=$${\frac{1}{8}=0.125}$$

「観測数4」の場合…「ある(実元a)」=$${\frac{15}{16}=0.9375}$$、「ない(純虚元$${b^4}$$)」=$${\frac{1}{16}=0.9375}$$
「観測数5」の場合…「ある(実元a)」=$${\frac{31}{32}=0.96875}$$、「ない(純虚元$${b^5}$$)」=$${\frac{1}{32}=0.03125}$$
「観測数10」の場合…「ある(実元a)」=$${\frac{1023}{1024}=0.9990234}$$、「ない(純虚元$${b^{10}}$$)」=$${\frac{1}{1024}=0.0009765625}$$

こうした考え方に基づいて、とりあえず母集団が正規分布(Normal Distribution)に基づくと考える頻度主義統計学は上卿の二項分布やポアソン分布について「観測数5~10」を統計学的事象の末端と認識しています(理論上一応は「観測数5」で5%水準、観測数10で1%水準をクリア?)。
数学的背景
例え巨大かつ一個しか存在しない対象でも、その観測には誤差がつきもの。ましや生物の群れや人間集団に至っては、自明の場合として最初からある程度の分散幅を備えて存在しています。
$$
誤差関数(ERror Function):erf(x)=\frac{2}{\sqrt{π}}\int_0^∞e^{-t^2}dt
$$

「統計学的事象」未満の事象とは要するに以下の様に視界のブレが激しく、しかもそのブレが観測者の手ブレのせいか観測対象の動きが激しいかの判別もつかない状態をいう。上卿の「十分に小さな領域は、まず「観測数1未満の世界=虚元=その他」に潜在する」な表現はこの状態に対応。

逆をいえば「観測数1」とは、この誤差e が隣の目盛りまで及ばない0<e<2の範囲で収まる状態を指すとも。まさしく整数(N進数)概念の出発点という訳である。
一方でこの様な状態は、不特定多数のベクトルがそれぞれ不定方向にランダムに伸ばされた単極球面体(尿道結石と覚えましょう)ともイメージ可能であり、その合成結果が半径1未満である限り、観測結果が0とも1とも(あるともないとも)つかない状態と看做す。
他方、この状態はまた確率論や情報理論では投げたコインがまだ空中を回転していて出目が表とも裏ともつかない「情報量1」の状態としてイメージされ、表か裏か出目が確定してして「情報量0」となる都度ベイズ更新が遂行される展開を迎える。

これが本当に安定してくるのはサンプルサイズ3000~10000前後から。この様に「サイズの壁」はまだ他にも存在する。


さらに付け加えるなら分散の方向は1次元だけとは限りません。


さらには線形でない可能性すら考えられ、そうやって多変数解析の世界への扉がおもむろに開かれるのです。こちら側の世界にようこそ?
直感的理解
とりあえずここまでで以下の3サイズが登場しました。
泡沫的事象(0<サイズ<2)
統計学的事象末端(サイズ5~10以上)
統計学的事象(サイズ3000~10000以上)

「泡沫的事象(0<サイズ<2)」と「統計学的事象末端(サイズ5~10以上)」の間に若干の隙間がありますが、まさにこのあたりにこそ「人間ドラマ」が展開する余地があるとも。
ところでチャールズ・ダーウィン(Charles Robert Darwin、1809年~1882年)は「種の起源(On the Origin of Species、1859年)」の中で「種とは確率論的推移による準安定状態の系統的推移である」と規定し、ノーバート・ウィナー(Norbert Wiener、1894年~1964年)も「サイバネティクス(Cybernetics、初版1948年、増補1961年)」の中でサイバネティクスなる学問の研究対象を「多種多様なフィードバックによって準安定状態を保ち続ける系」定義しましたが、概ねこれはここでいう「統計学的事象末端(サイズ3000以上)」の事と考えて良いでしょう。
この場合、「泡沫的事象(0<サイズ<2)」は「統計学的事象末端(サイズ5~10以上)」や「統計学的事象末端」に寄生しつつ、時には「統計学的事象末端」を構成しつつ「統計学的事象」に変化を与えていく存在と考えられそうです。それが良い内容にせよ、悪い内容にせよ。そもそも誰にとっての「良い」「悪い」なのかについてもちゃんと考えないといけませんね。さらに外部に「時宜の変遷」なる要素も設定しないといけませんし。
まだまだ全然仮組段階ですが「ミクロ的視野とマクロ的視野を連続させる(陰謀輪にも比較的強い)情報処理構造」の叩き台としては、まぁこんな感じでしょう。ここから先の展望としては、例えばマックス・ウェーバーの「鋼鉄の檻(Gehäuse)」理論と付き合わせてみるとか…
ドゥルーズ=ガタリのマシニック/メカニック論と付き合わせてみるとか…
ジル・ドゥルーズとフェリックス・ガタリは、『アンチ・オイディプス』や『千のプラトー』といった著作の中で「マシニック(machinic)」と「メカニック(mechanical)」という概念を対比させながら議論しています。この二つの概念は、彼らの哲学において重要な役割を果たし、特に「機械」と「システム」の概念を再定義し、人間、技術、社会の関係性を説明するために使われています。
1. メカニック(mechanical)とは
「メカニック」という概念は、従来の機械的なシステムや仕組みを指し、決まった動作、予測可能な動き、固定された構造を持つものを意味します。メカニカルなものは、通常、固定された部品や要素が一定の順序に従って動作し、外部からのエネルギーや入力によって機能します。つまり、時計やエンジンのような「閉じたシステム」として理解されます。
特性:
機能や動作があらかじめ決定されている。
外部の干渉に応じて変わることなく、内在する法則に従う。
機械の各部分が固定的に結びつき、分解可能。
2. マシニック(machinic)とは
これに対して「マシニック」は、ドゥルーズとガタリの特有の概念で、彼らは「機械」を単なる物理的な装置としてではなく、相互に連結し、関係性を形成し、生成と変化を含む動的なプロセスとして捉えます。マシニックなものは、固定された構造や機能を持たず、異なる要素が接続されたり切り離されたりする「開かれたシステム」として機能します。
特性:
創造的で動的、変化するプロセス。
固定された機能や目的を持たない。状況によって変化し、無限に変容する。
様々な要素が相互に影響を与え、結びつきながら新たな「組み合わせ」を生成。
生物、社会、物質、思想など、あらゆるものが「マシニックな集合体」を形成し、相互に接続して新しい生成を生み出す。
3. マシニックとメカニックの違い
ドゥルーズとガタリは、メカニックなものを「固定的で線形なシステム」として批判的に捉え、これに対してマシニックなものを「流動的で創発的なプロセス」として強調します。
固定性 vs 流動性: メカニックなシステムは既存の構造を維持し続ける一方で、マシニックなシステムは常に変化し、外部の要素を取り込みながら新たな結合や生成を行います。
決定性 vs 非決定性: メカニックなものは外部の力によって決定されるのに対し、マシニックなものは非決定的で、自己生成的なプロセスを含んでいます。
閉じたシステム vs 開かれたシステム: メカニックなシステムは部品の関係が固定されている閉じたシステムであるのに対し、マシニックなシステムは常に他のシステムや要素との関係を再編成し、開かれた形で動作します。
4. ドゥルーズ=ガタリのマシニックの例
欲望機械: 彼らの哲学における中心概念であり、欲望は人間の内面に閉じ込められたものではなく、様々な要素が結びついて生み出されるマシニックなプロセスです。欲望は他者や環境、物質との相互作用によって生成されます。
社会機械: 社会もまた、固定された構造や規則によって支配されるのではなく、マシニックなプロセスを通じて、様々な要素が連結され、新しい関係性が作られていく場です。
結論
ドゥルーズとガタリの「マシニック」は、従来の固定的な機械観を超えて、変動的で流動的なプロセスとして捉える概念です。メカニックなものが予測可能で固定的なシステムであるのに対し、マシニックなものは相互作用を通じて生成や変容が可能な動的なシステムを意味します。この区別は、彼らの哲学全体における動的で生成的な世界観を表現しています。
ダンバー数概念の導入も可能かも?
そんな感じで以下続報…
