
5年『四角形と三角形の面積』のデザイン①:平行四辺形の面積で「追究する学び」の素地づくり
これまでの記事で、5年生『四角形と三角形の面積』の単元での授業協力の準備を紹介してきました。その流れで、今回の記事では私が5年生を担任していた時の『四角形と三角形の面積』の単元の授業の記録について書こうと思います。
↓これまでの記事はこちらから御覧ください。
⓪単元のデザイン
多様な考えから公式化を導き、発展的に考える姿へ
『四角形と三角形の面積』の単元は、追究することを楽しみやすい単元です。
理由は、前回の記事でも述べた通り、単元内で「求積問題→公式化」のという流れの学びを繰り返すため、「こんな風に考えれば公式化できそうだぞ!」と単元内で学んだ手法を用いて考えることができるからです。
そのため、単元の導入段階では以下のことを大切にしようと考えます。
子ども自身の発想を大切にして、「多様な意見」を交流で取り上げる
公式化を焦らないで、「公式にしたい!」を引き出す
「底辺」「高さ」等の用語はしっかり確認して、使いこなせるようにする
一つひとつの項目の説明は、実際の授業の中でします。
本来なら5年生の中盤以降の単元ですので、必要のない内容かもしれません。しかし、この時担任していた5年生は、諸事情によりクラスごとではなく子どもを混ぜて授業をしており(しかも途中で繰り返しシャッフルします)、同じメンバーで算数の授業に取り組んでいませんでした。そのため、私自身が算数で大切にしたいことが浸透しているわけではないという事情がありました。
そのため、「集団で考えることで、見えてくれる楽しさを味わう算数授業」を改めて感じてもらおうと考えていました。
①1時間目
「面積は同じ?違う?」から問いを生む

1時間目の導入はミスコンセプション(誤概念)を生かして問いを生みます。
長方形を提示して「周りの長さは変えないで図形をたおしていくと…」と、長方形を平行四辺形へと変形します。そこで、「面積は同じ?違う?」と聞くと、両方の意見が出されました。

違うと答える子が多い一方で、同じと答える子もいる状況。つまり、学級内で意見が割れている状況は、「どちらなのだろう?」と子どもの問題意識が高まります。そこで、「まず分かっていることからはっきりさせようか。」と問うと、既習の長方形の面積の公式を用いて長方形の面積を求めました。
「ということは、この平行四辺形の面積が(5×6=)30㎠かそうではないかをはっきりさせればいいんだね!」と、平行四辺形の面積を求めるところに意識が向きます。そこで、「でも、平行四辺形の面積なんて求められるのかな?」と問い返しました。
「できる!」と答える子もいれば「えぇ…」と困った顔をする子もいて当然です。「困っている人もいそうだね。」とその様子を見て話していると、「先生!ジャキン!ガチャン!ですよ!」とある子が笑顔で声を上げます。
この「ジャキン!ガチャン!」はいわゆる等積変形の擬音なのですが、これを聞いた子どもたちにはよく分かったらしく「あぁ〜〜〜〜!そうだよね!」と盛り上がります。「これで分かりそうなら考えてみようか!」と促し、自力解決に入りました。その後の交流で出されたものが板書のものでした。

この2つは等積変形で考えやすいものです。黒板で子どもたちが変形し始めると「分かる!自分も同じ様に考えた!」と共感が生まれやすいものです。この考えを取り上げる中で「平行四辺形と長方形の面積は同じではないね!」とミスコンセプションは解消されていきます。
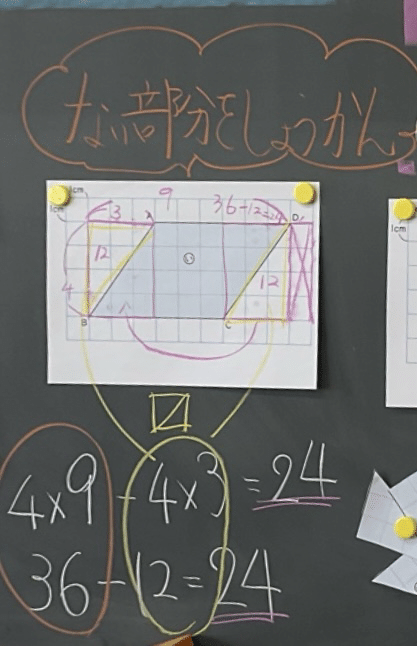
この考えは、「ジャキン!ガチャン!」を少し工夫しています。
平行四辺形を少し大きい長方形(赤い長方形)と見て、「ない部分をしょうかん」と本来求めるところではない部分を引く考えです。その部分は三角形になるのですが、三角形を組み合わせて長方形にすることで、うまく既習の長方形の公式が適用できるようにしています。
この頃には、子どもたちは「長方形にすれば公式が使えるから平行四辺形のめんsけいも求められる!」と、この単元で大切にしたい見方・考え方を働かせつつ、平行四辺形を捉えるようになってきています。

最後は「流れに合わないかも…。」と言いつつ挙手して発表した子の考えです。
黒板の線は少し違っているのですが、対角線ACで分割し、2つの三角形ABCとCDAを作ります。三角形ABCの頂点A、三角形CDAの頂点Cから垂線を下ろすと、合同な直角三角形が4つできます。その1つの直角三角形を板書の下の図形のように等積変形すると2×3=6㎠の長方形にすることができます。
つまり、6㎠×4つ=24㎠というわけです。この考えは、図らずしも直角三角形が長方形へ帰着しやすいこと(倍積ではないですが)ともつながっています。
子どもたちは「おもしろい!」「結局長方形にすればできる!」と話し、こうした独創的なアイデアを面白がっていました。
そして、「平行四辺形も長方形みたいに公式があればいいね。」「平行四辺形も公式あるんじゃない?」「なら円の面積の公式も欲しいな。」などと、授業の終盤はこれからどんなことを考えたいかを話しながら授業を終えました。
私は1時間目にこれからどんな図形を扱うかを示していないため、円の面積等も話題に上がります。(この会話が、単元終盤で見せる子どもたちの追究する姿につながっていきます。)
②2時間目
「平行四辺形の面積を求めて公式化できるかな?」
図形の構成要素に着目する

2時間目です。
子どもたちは前日で公式を作りたいと考えていたので、「公式ってどうして言える(どんなものだと言える)?」と初めに子どもたちに問いました。
(平行四辺形なら)どんな形でも当てはめられるもの
計算しやすいもの
言いやすいもの
子どもたちからはこのような返答がありました。
その内容は「式に表現したことを公式という簡潔・明瞭・的確な表現に高め(学習指導要領解説 算数編 p283)」ることで感じられることを指しています。
初めは唐突な問いで驚いたかもしれません。しかし、こうして「何のために公式として表すのか?」「公式にするよさにはどんなものがあるか?」を言語化して全体で共有することで、その後の公式を導く過程に拠り所が生まれます。
長方形の公式を例に、公式を作るために辺の長さが必要だということを考えました。(クラスの子どもたちは、長方形の公式が1㎠の数をかけ算で求めていることを思い出すまでに時間がかかりました。)そこで、「辺の長さとか、どこの長さを使ったのかをはっきりさせる必要があるね。」という声が生まれてきます。面積を求めることだけではなく、辺の長さといった図形の構成要素に着目し始めるのです。
新しい平行四辺形を提示し、面積を求めた結果を聞くと、多くの子は等積変形の考えで面積を求めていました。理由は、簡単で、どこの長さを使っているか分かりやすいからです。
2つの考えが出されると、「下の辺は「辺」でいいんだけど、長方形のたては辺じゃなくて…これこれ!」と2つの等積変形の考えで、共通している長さが話題になります。そこで、「これは高さっていうんだよ!」と伝えます。
合わせて「この高さはどんな線でもいいかな?」と問います。子どもたちは「長方形だから直角出ないといけないよ!」と、高さに必要な条件に気付きます。「ということは、下の辺に垂直な直線を「高さ」とすると下の辺とかけ算で求められるね。」と公式が見えてきます。
子どもたちは「たて×よこ」の長方形の公式に合わせて、「高さ×底辺」という公式化を行いました。
教科書では「底辺×高さ」ですが、初めからそこにこだわる必要はありません。
まず、優先して大切にしてあげたいのは「長方形の公式に帰着する」ということです。公式ありきで対応関係が見えないよりは、自分たちの言葉で考えた表現が分かりやすいはずです。実際、授業後、子どもたちの振り返りやその後の子どもたちとの会話で以下のような質問が複数ありました。
「平行四辺形の公式は「高さ×底辺」だってよく分かったんだ。でも、教科書とかドリルを見てみたら「底辺×高さ」って書いてあったんだよね。「高さ×底辺」の方が分かりやすいのになぜ「底辺×高さ」っていうの?」
子どもたちがだんだん自分の手で学びを深めようとしていることが伝わるでしょうか?
「教科書にあることを学ぶ」ではありません。
「教科書に載っている背景まで学ぶ」のです。
0から公式を考えていくことで、教科書に載っている知識との違いに気付きます。その気付きが自分たちの考えをより深め、豊かにしていくはずです。
なぜ「底辺×高さ」なのかは、高さを決めるには底辺を決める必要があるからです。
簡単な一言ですし、言ってしまえばすぐ伝わります。
しかし、「知りたい!」と思っている状態で聞くのか、急に説明されて「へぇ〜そんなんだ」と聞くのかでは、同じ知識が残っても「言葉1つにこだわって洗練する熱量」の伝わり方はきっと違うはずです。
「知りたいことが生まれる体験」も授業では大切にしたい体験です。
③3時間目
またまた「どちらの面積が大きいのかな?」

質問が多かった「なぜ高さ×底辺ではないのか?」から始めます。
「タワーの高さって?」と聞くと、「そりゃ、地面からてっぺんでしょ!」と。
「じゃあこんなオブジェの高さは?」「そりゃ、地面からてっぺんでしょ!!」
「では、平行四辺形の高さは?」「底辺から上の辺までかな?」「そうそう、底辺が分からないと高さって決められないんだよね。だから、急に「高さ」と言われても「どこの?」と思ってしまうから、先に「底辺」が来るんだよ。」と説明します。
子どもたちも納得です。
もちろん「自分たちが作った公式に愛着があるから、「高さ×底辺」がいいなぁ。」という子もいます。
その子は単元終了後のテストで、テスト中に「平行四辺形の公式を答えなさい。」という問題に「先生、これは一般的なものを答えた方がいいでしょうか?」と質問してきました。「どう思う?」と聞くと、「テストは一般的な方がいいです。」と答えてくれました。「もちろんその通りだよ。ただ、私はあなたが自分たちで公式をつくったということを覚えているし、そう質問するぐらいだからどう答えても大丈夫だよ。」と返すと、テストの答案用紙には「底辺×高さ」と解答してあり、その横に「私たちの授業では「高さ×底辺」」と書いてありました。
このやりとりが正しいのかは分かりません。
唯一、私の中ではっきりしているのは、授業の中で1から考えた取組は尊重してあげたいということです。
この話題の後、本題に入ります。
「どちらの平行四辺形の面積の方が大きいのかな?」という問題を出しました。
子どもたちは「マス目があればどんな平行四辺形でも求められるよ!」「意地悪な図形が来そうだな」などと話しています。
そこで、平行な直線をかき、その中に2つの平行四辺形をかきます。「底辺は?」という質問には「どちらも3cm」だと伝えます。
「高さは何センチ?」と聞かれるの「6cmだよ」を話します。
しかし、困ったような表情の子がいます。「どうしたの?」と聞くと、「アの平行四辺形とイの平行四辺形の高さって同じなのかな?」と疑問に思っていることを話してくれます。「もう少し詳しく教えて?」とイの図形にマス目を加えたものを掲示して話を聞きます。
「底辺に垂直だから…」と赤い直線部分を示し、「これを高さにしてもいいの?」とみんなに問いかけました。
このようにして、「どちらが大きいか?」を問うことで、自然と子どもたちの思考は「面積を求めたい!」と進んでいきます。その中で、「今までの公式の高さは図形の中にあったのに、高さを図形の外に見いだしても良いのだろうか?」と自然と問いが生まれてくるのです。
その子の問いを聞いた子が、「それなら、また「ウイーンガシャン!」をして確かめてみれば良いよ!」とその解決策を話します。
この一言で、「今までの公式の高さは図形の中にあったのに、高さを図形の外に見いだしても良いのだろうか?」というその子の問いが、「等積変形等の考え方で面積を求めることができれば、図形の外に高さ見いだして公式を適用できるはずだ」という全体の追究する<問い>へと変わりました。
子どもの考えは板書にある通りです。
下に掲示されている考えはこれまでの既習を上手に活用しています。
高さが図形の中にあるよう「分割」にして面積を求める
長方形と見立てて「分割」して面積を求める
高さが図形の中にあるように「等積変形」して面積を求める
これらが考えが出されたことで「面積も一緒だから、高さが外にあっても大丈夫だね!」と<問い>が解決されます。
そして、右上の考えが「斜めに切って動かせばいいよ!」といいながら出されました。
「面積が同じということは、こうやって切って図形を変形させればアと同じ図形になるよ!」と説明してくれました。些細な点かもしれませんが、「ほんとだ!」と盛り上がって授業を終えます。
以上が『四角形と三角形の面積』の平行四辺形の内容でした。
1つの記事でまとめ切ることは難しいです。
この記事で見えてきた、子どもが「追究する学び」の素地は以下のようにまとめていくことができます。
自分で考えを進めていくことができるか
考えたいと思えるか
考え始め、困ったことを表出できるか
困ったり、考えたことについて、それを一緒に考える集団であるか
これらを総合してみると、個人の学びとして完結するのではなく、個人の学びが集団で学び方となり、更に個人として還るようなものとしてとらえることができます。
このような学びの過程がなぜ「追究する学び」と結びつくのか。心理学者の鹿毛雅治は『モチベーションの心理学』の中で、以下のように指摘しています。
グループでの共通の目標を持つことが社会的な結束を促し、学習に対するモチベーションのみならず、責任や援助を基盤とする社会的なモチベーションをも高める。そのことによって、メンバー同士のコミュ二ケーションや援助行動といった社会的相互作用が促され、効果的な社会的な相互作用パターン(たとえば、相互信頼に基づく行為、情報や道具のシェア、効果的な援助やフィードバックの提供、励まし合い、相互説明、複眼的な視点の共有など)が生じ、ひいてはパフォーマンスが向上する。
解決したい「問い」がこの指摘の中では「目標」と同じものとして考えられます。その問いが、「学習に対するモチベーション」=「追究する学び」へとつながるのです。
しかし、それだけでは学びを深めることは単元の導入段階では難しいです。そこに「効果的な社会的な相互作用パターン(多様な面積の求め方、困りの表出と解決方法の提示、)」が加わることで、「追究する学びの仕方」が子どもたちにもみえてきます。
平行四辺形の内容では、「追究する学び方」を見つけていく段階だといえます。面積の求め方には慣れてきましたが、公式化を自由に考えられる状態ではありません。「追究する学び方」をつかみ、少しずつ試していくことで、自分の手で追究していくことができるようになるのです。
最後まで読んでいただき、ありがとうございます。
