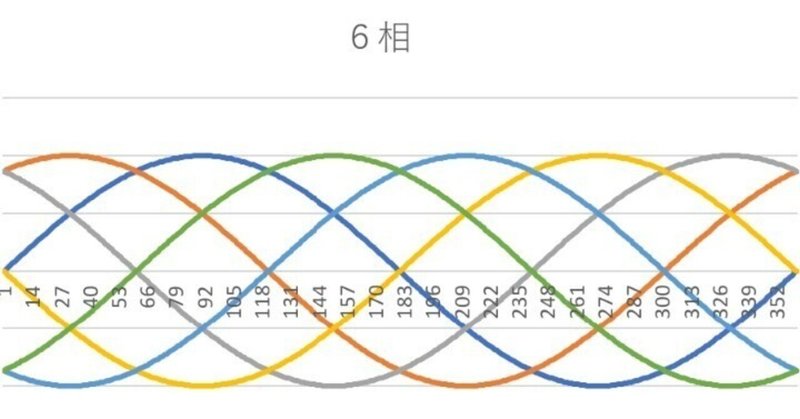
６相６線式送電線路を考える(3)　「複素数で計算」

それでは今回は、各電圧をもっと簡単に計算したいと思います。

3相３線式の各電圧

A相、B相、C相それぞれの相電圧(前回のおさらい)

$$
\begin{aligned}
v_A &= E \sqrt{2} \sin \left(\omega t + \dfrac{1}{6}\pi \right) &\text{…(8-A)}
\\\\
v_B &= E \sqrt{2} \sin \left(\omega t + \dfrac{5}{6}\pi \right) &\text{…(8-B)}
\\\\
v_C &= E \sqrt{2}  \sin \left(\omega t + \dfrac{3}{2}\pi \right) &\text{…(8-C)}
\end{aligned}
$$

A-B間、B-C間、C-A間それぞれの線間電圧

$$
\begin{align*}
v_{AB}&= \sqrt{3} E×\sqrt{2}  \sin \omega t &\text{…(9-1)}
\\\\
v_{BC}&= \sqrt{3}  E ×\sqrt{2}  \sin \left(\omega t + \dfrac{2}{3}\pi \right) &\text{…(9-2)}
\\\\
v_{CA}&= \sqrt{3}  E ×\sqrt{2}  \sin \left(\omega t + \dfrac{4}{3}\pi \right) &\text{…(9-3)}
\end{align*}
$$

ベクトルで計算すると楽

上の式を交流の瞬時値と言います。
関数を使い、変化し続ける電圧を正しく表しているのですが、計算が面倒です。
そこで次のようなベクトルの式を使います。

$$
\begin{align*}
\.{V_{A}}&=E  \angle \dfrac{1}{6}\pi
\text{　←極座標表示　Eが絶対値で、}\frac{1}{6}\pi\text{は偏角}
\\\\
&=E \left(\cos\dfrac{1}{6}\pi + j \sin\dfrac{1}{6}\pi \right)
\\\\
&=E \left(\dfrac{\sqrt{3}}{2} + j\dfrac{1}{2}\right)\text{　←直交座標表示}
\end{align*}
$$

$${\.{V_{A}}}$$はA相の相電圧のベクトル、 $${E}$$ は相電圧、
$${j = \sqrt{-1}}$$
※数学では $${i}$$を使いますが、電気では電流と紛らわしいので$${j}$$を使います。

まず、$${\sqrt{2}}$$が消えました。
これは瞬時値のときは、
最大値 = 実効値$${× \sqrt{2}}$$
のため必要だったのですが、交流のベクトルのときは実効値と位相だけでいいのでいらなくなりました。
それでも sin と cos が出てきますし、複素数に慣れなければなりませんが、慣れればこちらのほうがずっと楽です。
理由①　図で整理され分かりやすい。
理由②　単位ベクトルを掛けると回転させられる。(単位ベクトルは絶対値が1の複素数)

ベクトル式は、電源を入れてしばらく後の安定した状態の計算を簡単にする方法なのです。
このように交流の計算は通常、複素数を使い2次元で計算します。

早速ベクトルで計算してみます。

相電圧はこうなります

$$
\begin{aligned}
\.V_A &=E  \angle \frac{1}{6}\pi\\\\
\.V_A&=E \left(\dfrac{\sqrt{3}}{2} + j\dfrac{1}{2}\right)\text{　…(10-A)}\\\\\\
\.V_B &=E  \angle \frac{5}{6}\pi \\\\
\.V_B &=E \left(-\dfrac{\sqrt{3}}{2} + j\dfrac{1}{2}\right)\text{　…(10-B)}\\\\\\
\.V_C &=E  \angle \frac{3}{2}\pi \\\\
\.V_C &= -jE \text{　…(10-C)}
\end{aligned}
$$

線間電圧はこうなります

$$
\begin{aligned}
V &= E \sqrt{3}\text{とおくと、} \\\\\\
\.V_{AB}&=V \angle 0 \\\\
\.V_{AB}&=V \text{　…(11-1)} \\\\\\
\.V_{BC}&=V \angle \frac{2}{3}\pi \\\\
\.V_{BC}&=V \left( -\dfrac{1}{2} + j\dfrac{\sqrt{3}}{2}\right)
\text{　…(11-2)}\\\\\\
\.V_{CA}&=V \angle \frac{4}{3}\pi \\\\
\.V_{CA}&=V \left( -\dfrac{1}{2} - j\dfrac{\sqrt{3}}{2}\right)\text{　…(11-3)}
\end{aligned}
$$

各電圧のベクトル図

ここから下は線間電圧の計算です

Ａ−Ｂ間の線間電圧の計算

$$
\begin{aligned}
\.V_{AB}&=\.{V_{A}}-\.{V_{B}}
\\\\
&=E  \angle \dfrac{1}{6}\pi - E  \angle \dfrac{5}{6}\pi
\\\\
&=E  \left\{\left(\cos \dfrac{1}{6}\pi + j\sin \dfrac{1}{6}\pi \right) - \left( \cos \dfrac{5}{6}\pi + j\sin \dfrac{5}{6}\pi \right)\right\}
\\\\
&=E \left\{\left(
\dfrac{\sqrt{3}}{2} + j\dfrac{1}{2}
\right)-\left(
-\dfrac{\sqrt{3}}{2} + j\dfrac{1}{2}
\right)\right\}
\\\\
&=E \left(
\dfrac{\sqrt{3}}{2} + j\dfrac{1}{2}
+\dfrac{\sqrt{3}}{2} - j\dfrac{1}{2}
\right)
\\\\
&=E \sqrt{3}
\\\\
V &= E \sqrt{3}\text{とおくと、}
\\\\
\.V_{AB}&=V \text{　…(11-1)}
\end{aligned}
$$

Ａ−Ｂ間の線間電圧は相電圧のベクトル合成

Ｂ−Ｃ間の線間電圧の計算

$$
\begin{aligned}
\.V_{BC}&= \.{V_{B}} - \.{V_{C}}
\\\\
&=E  \angle \dfrac{5}{6}\pi - E  \angle \dfrac{3}{2}\pi
\\\\
&=E \left\{\left(\cos\frac{5}{6}\pi + j\sin\frac{5}{6}\pi\right)-\left(\cos\frac{3}{2}\pi + j\sin \frac{3}{2}\pi \right)\right\}
\\\\
&=E \left\{\left(-\dfrac{\sqrt{3}}{2} + j\dfrac{1}{2}
\right)-\left(0 - j \right)\right\}
\\\\
&=E \left( -\dfrac{\sqrt{3}}{2} + j\dfrac{1}{2}
 - 0 + j \right)
\\\\
&=E \left( -\dfrac{\sqrt{3}}{2} + j\dfrac{3}{2}\right)
\end{aligned}
$$

ここで()内の絶対値を1にするため、以下の公式を使います。

$$
\alpha \cos \theta + j \beta \sin \theta
=\sqrt{\alpha^2 + \beta^2}\left(
a \cos \theta + j b \sin \theta \right)
$$

ただし、$${(a \cos \theta)^2 + (b \sin \theta )^2 = 1}$$

$${\sqrt{\alpha^2 + \beta^2}}$$は絶対値(ベクトルの長さ)を表し、
$${a \cos \theta + b \sin \theta )}$$は基準ベクトルを0゜としたときの位相角(ベクトルの偏角)を表します。

$$
\begin{aligned}
 \sqrt{\left(-\dfrac{\sqrt{3}}{2}\right)^2 + \left(\dfrac{3}{2}\right)^2}
&=\sqrt{\dfrac{3}{4} + \dfrac{9}{4}}
\\\\
&=\sqrt{\dfrac{12}{4}}
\\\\
&=\sqrt{3}
\end{aligned}
$$

$$
\begin{aligned}
\.V_{BC}&=E \sqrt{3} \left( -\dfrac{1}{2} + j\dfrac{\sqrt{3}}{2}\right)\\\\
\.V_{BC}&=V \left( -\dfrac{1}{2} + j\dfrac{\sqrt{3}}{2}\right)\text{　…(11-2)}
\end{aligned}
$$

Ｃ−Ａ間の線間電圧の計算

$$
\begin{aligned}
\.V_{CA}&= \.{V_{C}} - \.{V_{A}}\\\\
&=E  \angle \dfrac{3}{2}\pi - E  \angle \dfrac{1}{6}\pi
\\\\
&=E \left\{\left(\cos\frac{3}{2}\pi
+ j\sin\frac{3}{2}\pi\right)
-\left(\cos\frac{1}{6}\pi
+ j\sin \frac{1}{6}\pi \right)\right\}
\\\\
&=E \left\{\left( 0 - j \right) -
\left(\dfrac{\sqrt{3}}{2} + j \dfrac{3}{2}\right)\right\}
\\\\
&=E \left( -j -\dfrac{\sqrt{3}}{2} - j\dfrac{1}{2} \right)
\\\\
&=E \left( -\dfrac{\sqrt{3}}{2} - j\dfrac{3}{2}\right)
\end{aligned}
\\\
\\
\begin{aligned}
 \sqrt{\left(-\dfrac{\sqrt{3}}{2}\right)^2 + \left(\dfrac{3}{2}\right)^2}&=\sqrt{\dfrac{3}{4} + \dfrac{9}{4}}\\\\&=\sqrt{\dfrac{12}{4}}\\\\&=\sqrt{3}\end{aligned}
$$

$$
\begin{aligned}
\.V_{CA}&=E \sqrt{3} \left( -\dfrac{1}{2} - j\dfrac{\sqrt{3}}{2}\right)\\\\
\.V_{CA}&=V \left( -\dfrac{1}{2} - j\dfrac{\sqrt{3}}{2}\right)\text{　…(11-3)}
\end{aligned}
$$

読んでいただき、ありがとうございます。

続き↓