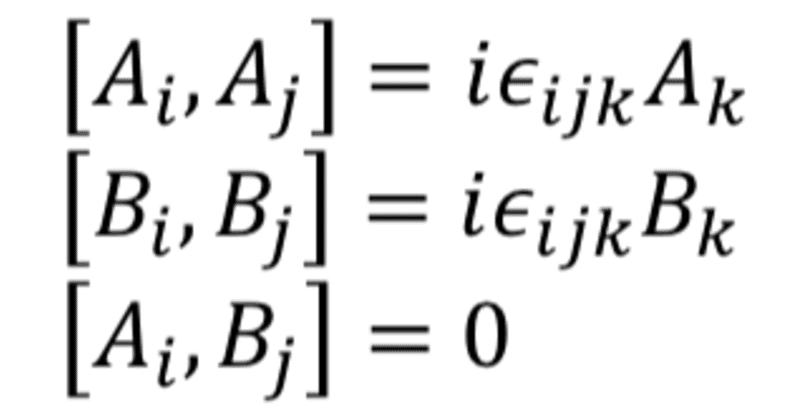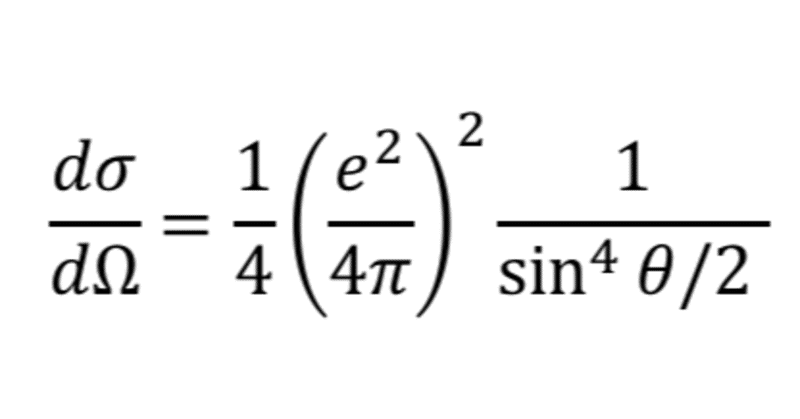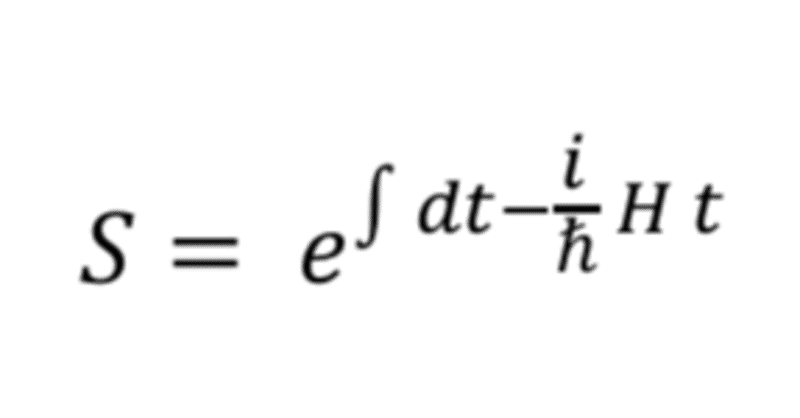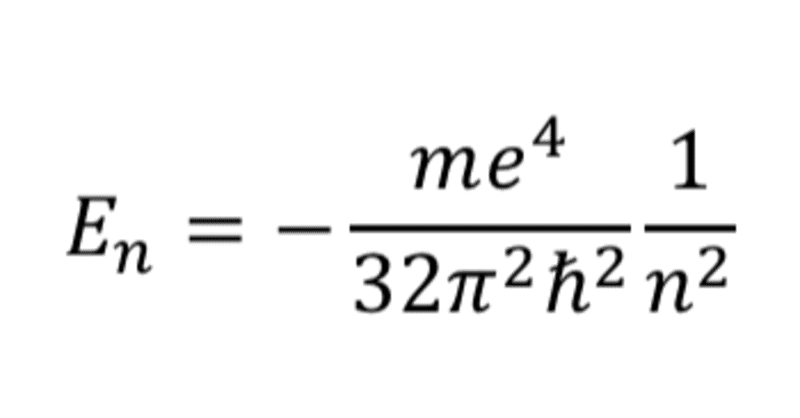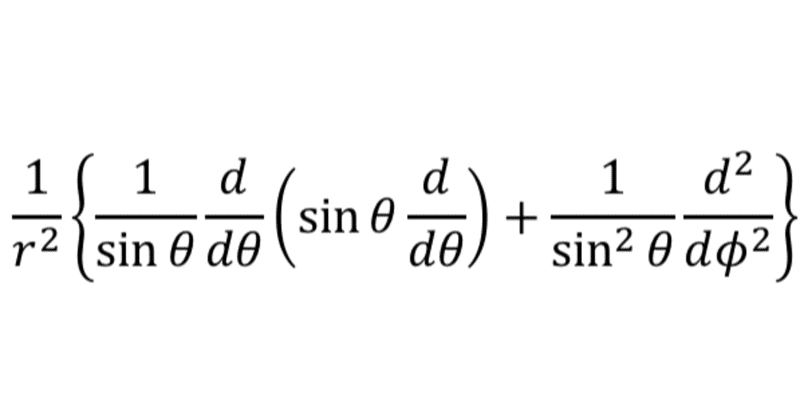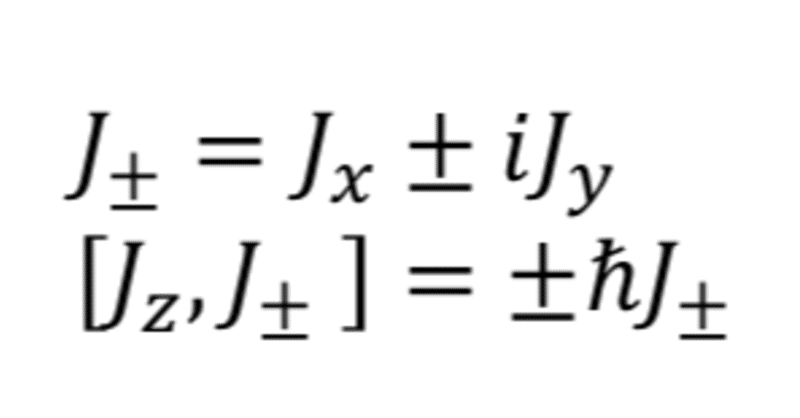記事一覧
スピンの源:お話物理:場の理論
前回は量子力学の粒子描像を捨て,時空の各点にある場の励起が粒子であるという立場を取ることにした.
今回は相対論的に許される場は何があるのかについて話していこうと思う.
高エネルギーの物理を考えていく上で理論が相対論的に対してよく振舞わなければならない.新しい理論を作るなら,今までの成功している理論に従う必要があるのだ.
特殊相対論は時間+空間の計四次元の回転で記述される理論だ.回転の議論は量
生まれる粒子終わる量子力学:お話物理:粒子描像の終わり
前回までは,量子力学の散乱問題を扱ってきた.摂動論というシステマティックな近似計算を使えば,人間が計算できる限り,実験の求める精度まで,実験と比較できる物理量を計算できるのだった.その物理量と実験の比較から粒子間の相互作用を決められるのだ.
ではこれで物理は終わりか.この世にある全ての粒子の組み合わせを,実験の精度の限り,相互作用のリストを作れば終わりになるのだろうか.
幸か不幸か,答えは"否
より小さきを知るには:お話物理:弾性散乱
前回までで,量子力学の散乱問題を摂動論で扱ってきた.粒子同士の相互作用:ポテンシャルを仮定することで,実験と比較できる散乱断面積を計算することができた.
電子-陽子散乱断面積
を計算して,実際に実験を行い,どの精度でこのポテンシャルが現実を再現しているかを確かめられるのだ.
逆に実験の精度をあげれば,いずれこの計算と実験のズレが生じる.このズレはどこからきているのか.それは摂動計算という近似
飛び散り方:お話物理:摂動論
前回までのお話物理で,散乱を記述するS行列をなんとか人間が計算する為に,摂動展開と言う,近似計算を始めたのだった.
散乱問題の摂動計算として,自由粒子がポテンシャル"V"の摂動を受ける状況を考えたのだった.
青の部分はVの影響を受けずそのまま素通りする部分,赤の部分がVの影響を一回受けて散乱される,最低次の部分だ.
今回は電子-陽子散乱の具体的なハミルトニアン
で摂動の最低次がどうなるか,
ちょびっと影響:お話物理:摂動論
前回までのお話物理では,散乱を記述する為にはS行列を計算すればよかったのだった.しかし人間にはS行列の正確なものを計算するのはとても大変で,実質不可能なのだった.しかし完全な計算を実行できなくても,なんとかそれっぽい計算方法を考えたい.そうでなければ物理という学問はおしまいだ.
さて今回からようやく実際の計算をして行こうと思う.完全な計算ができないなら,なんらかの近似をすることになる.近似とは,
絵に描いたもち:お話物理:摂動論のさわり
前回までは,粒子の性質を探る方法について話してきた.目に見えない粒子の性質を探るには,粒子をぶつけて,飛び散りかたを見るのだった.
そのデモンストレーションとして,陽子-電子散乱の話を始めたのだった.陽子-電子の系は,水素原子と同じハミルトニアンで指定される.ただ,電子が陽子に囚われているのが水素,これから考えるのは電子のもつエネルギーが高く,囚われない状態を考えるのだ.
散乱を考えるときは,
大きさ:お話物理:電子-陽子散乱
今回から,陽子の"大きさ"の話をしようと思う.
実験的に,目に見えない粒子の大きさはどうやって決められるのだろうか.実験的に決める方法がなければ理論的にいくら計算(予想)したところで意味がない.ただの妄想と区別がつかない.
これから話すのは"陽子の大きさ"を導入した簡単な量子力学の問題を用意して,実験的に測定できるものを計算する.その計算を実験で実際に測定したものと比べることで陽子の"大きさ"
見えないものを探る行列:お話物理:散乱
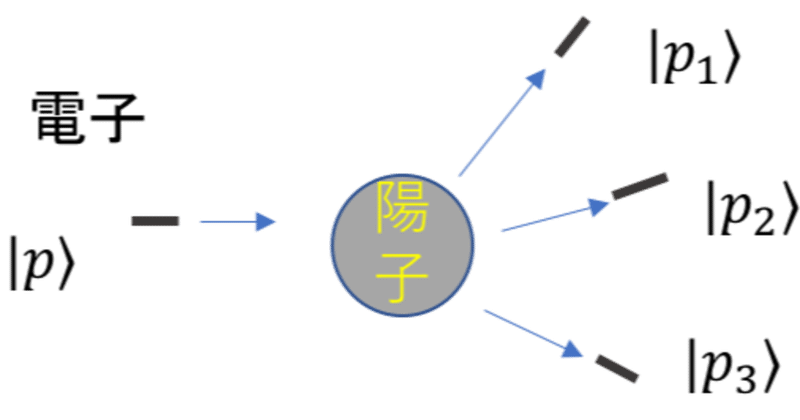
前回は,物理屋が小さなものを見るときにどうするかの話を始めたのだった.素粒子の性質を知るには,目に見えない,手を触れられないものの性質を知らねばならない.見ることも触れることもできないものに弾丸を撃ち込んで,飛び散ったものを見て,物理屋はその性質を探るのだった.
今日はその弾丸とは何か,飛び散ったものは何か,飛び散ったものから箱の中身を探る方法について,もう少し物理っぽく話をしようと思う.
は
あなた二人で居たい:お話物理:水素様原子
前回までは,水素原子の量子力学を解いてきた.固有値方程式からエネルギー固有状態を作ることに成功して,いくつかの具体的な波動関数の形をみたのだった.
そして,水素原子の最低エネルギー状態とは,古典的には潰れてしまい受け入れられなかった,原子核に電子が落ち込んでいる状態だった.水素原子の大きさは量子力学的な"ぼやけ"によって保証されているのだ.
今回は,一般の原子を作っていこうと思う.
一般の原
落ちているのに落ちてない:お話物理:水素原子
前回は,水素原子のエネルギー固有値が,動径方向の固有値方程式の規格化可能性から,跳び跳びの値を取ることを話したのだった.
正数"n"が動径方向の波動関数から決まる,量子数なのだった.
今回は具体的な波動関数の形をみて,言えることを考えてみよう.
動径方向の波動関数は,角運動量の大きさ"l"に依る微分方程式
から決まる.昔の数学者がこの微分方程式の解を見つけてくれている.
具体的に書き下せ
跳び跳びのエネルギー:お話物理:水素原子
前回は,我々を構成する原子のもっとも簡単な模型である,水素原子の話を始めたのだった.古典的には,原子核の周りを電子は楕円軌道で回るのだが,それを認めると,原子が潰れて大きさを持てなくなってしまったり,跳び跳びの色の光が出てくる実験結果と合わないのだった.
水素原子のハミルトニアンは
という形だった.三次元の固有値方程式は
という形になる.長い.
長い数式を見るとうんざりする.がじっと見ると
跳び跳びの色:お話物理:水素原子
さて前回までで,球面調和関数と呼ばれる関数を作った.三次元の回転対称な量子力学方程式の話の準備をしてきた.
今回からその準備から,水素原子の話をしよう.
水素原子は我々を構成している原子のもっとも簡単なシステムだ.
しかしその水素原子は古典的に電磁波を放出して原子核に電子が落ち込んでしまう.そのせいで長い時間,人間が人生を歩めるほどの時間,原子が大きさを持てないのだ.
水素原子が安定して存
回る方程式:量子力学:極座標のschrodinger 方程式
前回は,角運動量の固有状態について話してきた.角運動量固有状態は角運動量の大きさ"J^2"と一成分"J_z"が決められるのだった.
上では状態のラベルとして固有値"λ","m"で書いているが,今後は
と書こう.
この固有状態で特別なことは,角運動量の大きさ"j"が0または半整数(整数/2)であること,一成分の値が"-j"から"j"までの"1"刻みでしか取れないことだ.
この二つの跳び跳びの
昇り降りと跳び跳びの値:量子力学:角運動量
前回までで,量子力学の角運動量は回転の無限小生成子として導入したものの,その交換関係が0でないことから,状態として同時に決められるのが"J^2"と"J_z"の二つであることがわかった.
古典的には矢印の形で決められた角運動量は,量子力学では長さと一成分しか決められないのだ.
今回は角運動量固有状態の固有値について見ていこう.
とりあえずおもむろに,次のような固有状態
と,昇降演算子を考える