
【高校情報Ⅰ】計算誤差/Pythonプログラミング(コンピュータの仕組み)動画解説/教員研修用教材 学習11
文部科学省提供 高等学校情報Ⅰ
教員研修用教材の第3章コンピュータとプログラミング
学習11 コンピュータの仕組み(計算誤差)に完全対応
誤差のPythonプログラム部分は、教員研修用教材のみの内容だと、基本情報技術者試験を合格していても理解できる人は少ないと感じたため、
今回も、教材の内容をベースに、かなり補足説明を追加しています。
誤差の種類は研修用教材には記載はないですが、情報処理試験では誤差説明で必ずでてくるので、一緒に解説追加しました。
■■動画解説■■
情報Ⅰ共通テスト対策 書籍出版します!
■■文字おこし■■
がっきー 大変 お風呂のお湯があふれているよ~止め忘れた~

お風呂の容量を超えたから溢れたんだね。
またまた、難しい表現使いますなあ~
コンピューターの世界にもオーバーフローと言って、容量オーバーすることがあるんだ。

へぇ~ 具体的にどんな感じなの?
以前説明したように、コンピューターの世界は0と1の2進法であらわす。
この1桁を1ビットっていうんだ。ビットはデータ量を表す単位なんだ。
よく、スマートフォンとかの容量を表すのに、何とかバイトって聞いたことない?
実は、コンピューターの世界では8ビットは1バイトとして定義されるんだ。
以前のPython講座でやった変数の箱を例に説明するね


例えば
13ビットの容量がある魚Aがいたとする。
それを15ビットの容量がある箱に入れたとしたらどうなる?
ちゃんと箱の中に魚が収まるね。
じゃあ、20ビットの容量がある魚Bがいたとする。
箱に収まるかな?
15ビット分は収まるけど 5ビット分は失われてしまうね。
そうなんだ、その失われた5ビットを誤差というんだ。
実際の計算式でいうと
例えば
1÷3は0.33333・・と永遠に割り切れずに3が続くよね
これと同じように2進法でも
例えば10進法の0.1を2進法にすると
0.0001100・・と無限に終わらない。
コンピュータの容量は有限だから、どこかで無理やり終わらせる必要がある。
1
誤差の種類については、何種類かあるから説明するね。

まずは、けたあふれ誤差
演算した結果が、コンピュータの扱える最大値や最小値を超えることによって生じる誤差なんだ
扱える最小値をMin 最大値をMaxとして
最小値を超えてしまうことをアンダーフロー 最大値を超えてしまうことをオーバーフローと呼ぶ

次に情報落ち というのがある
絶対値の大きな値と絶対値の小さな値の加減算を行ったときに絶対値の小さな値が計算結果に反映されないという誤差のことなんだ
う~ん、言葉だけでは意味が分からない
具体的な値で説明するね。分かりやすくするために二進法ではなく、十進法でやるね
たとえば
0.1234×10の4乗と0.5678×10のマイナス4乗の足し算を考えてみよう
小数点以下の有効桁数は4桁
このとき 足し算をするためには指数部をそろえないといけないから
どちらも10の4乗であらわすと
0.1234×10の4乗と
0.000000005678×10の4乗となる。
計算結果は
0.123400005678×10の4乗だけど
小数点以下の有効桁数は4桁だから0.1234×10の4乗となり小さな桁の方ははみ出てしまって、誤差として情報が落ちてしまうことを情報落ちというんだ。

次に打切り誤差
計算処理を、完了まで待たずに途中で打ち切ることによって生じる誤差が
打切り誤差なんだ
これは3.1415・・の円周率が良い例になる。
になる

次に、けた落ち
絶対値がほぼ等しい数値同士の差を求めた時に有効な桁数が大きく減ることによって生じる誤差を桁落ちという
例えば0.555×10の7乗の有効桁数は小数点以下の3桁
0.554×10の7乗の有効桁数も小数点以下の3けた
これの差を求めると0.001×10の7乗となり有効桁数は1けたとなる
正規化すると
0.100×10の5乗と自動で00が付加されるわけだけど、この桁が元々0だったという保証がない つまり信用できない桁が増えるのが、けた落ちなんだ

最後に丸め誤差
表現できる桁数を超えてしまったために、最小桁より小さい部分について四捨五入や切り捨て、切り上げなどを行うことによって生じる誤差を丸め誤差という
たとえばこんな風に
1.0011010 が永遠に続く場合、どこかの桁で切り捨てを行う行為になる。
じゃあ、こんどはプログラミングで誤差を体験していこう。
他の動画でアップしているPythonの超入門講座は理解していることを前提にすすめるね。

以前、Pythonの型について説明したときに
数値は小数点を含まない「整数」と小数点を含むもののどちらかで扱われるとはなしたよね。
そして、その扱う型を整数はINT型、浮動小数点数はFloat型を使うと話した。
ちなみに、固定小数点数はdecimal型というのを使う。
この型もさっき話したように扱える値の最大値が決まっているんだ。
プログラミング言語によっては、整数や小数で扱えるビット数が異なる型が色々用意されている。無駄に大きい箱を準備してしまうとその分メモリを使ってしまうから、扱う想定のデータ量によってあらかじめ使う型を決めたりする。
#float型の誤差
import sys
x = sys.float_info.max
print(x)フロート型で試していこう。
まず、import sys でsysライブラリを読み込む。このライブラリの中にフロート型の最大値を返す関数(機能)があるんだ。
実際に記載していこう
sys.float_info.max で sysライブラリのfloat_infoという機能の集まりの中の、maxというfloat型の最大値を返却する機能呼び出しを行う。
これは最大値を返却するから 変数x に代入する。
その値を print文で表示させてみよう。 実行するね。

あれ? 最後のe+308 ってなに?数字なのに英語のe とか わけわかんないんだけど
eという表示は、10のべき乗という意味なんだ。eの後に何乗するかを記載する
e+308は 10の308乗という意味
例えば
3.2e+3 は、3.2×10の3乗の意味で計算すると3200になる。
eの隣をマイナスにすると、10のマイナス 〇乗の意味なる
例えば3.2e-3は 10のマイナス3乗だから 0.0032となる
#float型の最大値の末尾に9を5つ付与
x = 1.797693134862315799999e+308
print(x)じゃあ、今度はFloat型の最大値を手入力で入れてみて そのあとに5桁 9を入れてみよう
プリントxで表示させてみよう

Float型で扱える桁数をオーバーしたからついかした5桁の9が切り捨てられたね。
#float型の最大値を超える値
x = 1.8e+308
print(x)
じゃあ今度は、Float型の最大値を超える値を入れてみよう。
1.8e+308 を変数xに代入して
これを表示させてみよう

あっ!Inf と表示された
これはさっき説明したオーバーフローの意味で、扱える値の最大値を超えたからエラーなったんだ。
じゃあ、今度は整数だけで減算した結果と小数だけで減算した結果で誤差を確認していこう

Pythonのプログラムで
28―27はなんだと思う
1に決まってるじゃん
じゃあ、実行してみよう。ちゃんと1って表示されたね
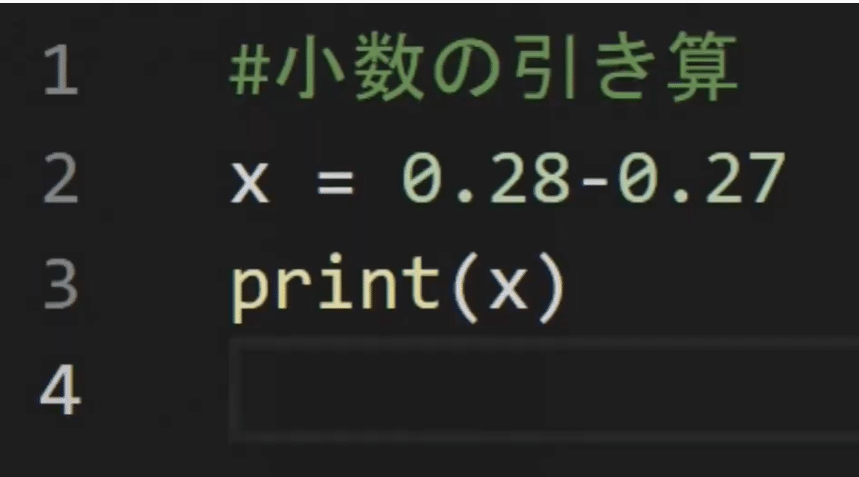
じゃあ、0.28―0.27はなんだ
0.01に決まっているじゃん

じゃあ、実行してみよう
あれ?おもったのとちがう 最後の9ってなに?

これが、誤差なんだ、
計算式自体は、十進法であらわしているけど、前に話したようにコンピュータの世界では
一度0と1の2進法にする必要がある。
0.28や0.27は 二進法に変換すると、無限に数が続くからどこかの桁までで終わりにしないといけない。
つまりその、ちょん切った後の数値分は計算されないから誤差が発生するんだ。
へぇ~奥が深い。
じゃあ、これを正しく計算させるにはどうしたらいいの?

いい質問だね。
小数だと今回のような誤差が発生する可能性があるから、一度整数に直して 計算後に小数に戻すやり方がある。
0.28に100をかけて28の整数にする。
0.27も同じように100をかけて27の整数にする。
28-27をした後に100で割れば誤差が起こらない。
この誤差は、扱いを間違うと大きなトラブルになりかねない。
例えば、惑星探査機が地球から木星まで行って帰る軌道計算に使用した場合、この誤差があるとどうなると思う?
地球から木星ってすごい距離があるから、わずかな角度の差、スピードの違いが、
航行(こうこう)を続けるうちに大きな影響を与えるね。
そうだね。あと惑星探査には地球重力圏からの脱出、地球以外の惑星の重力を利用してスピードをあげるスイングバイ航行、目的とする惑星に近づいた際の速度や軌道の調整など、膨大な計算が必要になるため、大きな問題になる可能性がある。
今話した誤差は、プログラミングするうえで大切な知識になるからしっかり覚えておこう。
この記事が気に入ったらサポートをしてみませんか?
