
【実践例】プログラミングで正多角形を学ぶ
今回はプログラミングで正多角形を学んだ実践例についてご紹介いたします。実際に東京コミュニティスクールの小学5・6年生と算数の学びの中でプログラミングを使いながら「正多角形」の単元を学びました。
基本的な学びの方針
学びの流れとしては、「個別事例」から「一般法則」を考え、最終的には「アート作品を作り上げる」ところまで行います。帰納的な推論を使ってプログラムに活かす、そんな学びです。
学びの流れ
1.正三角形から、正七角形までの正多角形をノートに作図し、特徴をまとめる。
2.正三角形、正方形、正五角形をプログラムで描く
3.どんな正多角形でも描けるようなプログラムを書く
4.パターンブロックを使ってA4用紙を敷き詰めるパターンのある文様をつくる
5.パターンブロックでつくった文様をプログラムで実装する
1.正三角形から、正七角形までの正多角形をノートに作図し、特徴をまとめる。
まずは「書いてみる」ことは多分に必要となります。いままで意識せずに書かなかった正多角形。作図して、それぞれの特徴をまとめていくとだんだん規則性が見えてきます。
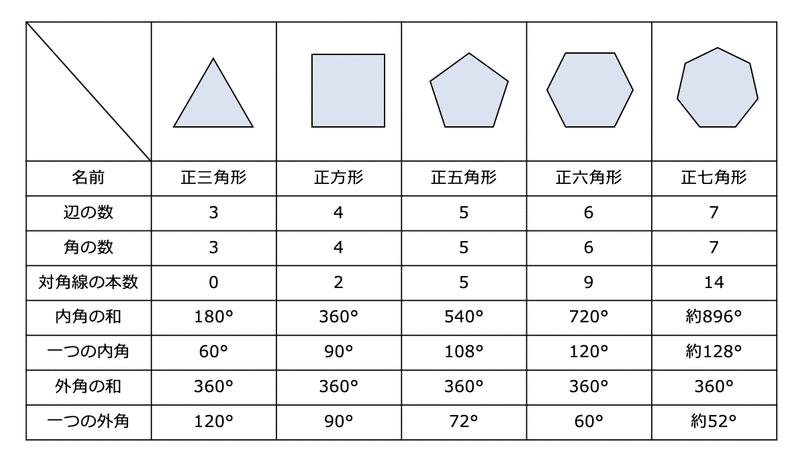
外角の和は常に一定で 360度であること、そこからその他の計算が導けること、そして対角線の本数も実際に手で書いてみると、
「あ、一つの頂点からその頂点の隣以外に線が引ける!」ということに気づき、一歩一歩抽象化の階段をのぼることができます。
2.正三角形、正方形、正五角形をプログラムで描く
次は、学んだ規則性を活かして、プログラムで図形を書いていきます。まずは簡単な正三角形、正方形、正五角形から。ピョンキーというプログラミング言語を使って書いていきます。
正方形はすごく簡単に書くことができるのですが、ここで起こる「既有知識」と「プログラミング」の齟齬に出会います。
多くの子供達はまず「内角」分だけ、スプライトを回せば良いと認識します。上に上げた3つの打ち内角と外角が一致しているのは、正方形だけなので、正三角形を描こうとして「正六角形」を描いてしまったり、正五角形を描こうとして「星印」を描いてしまいます。
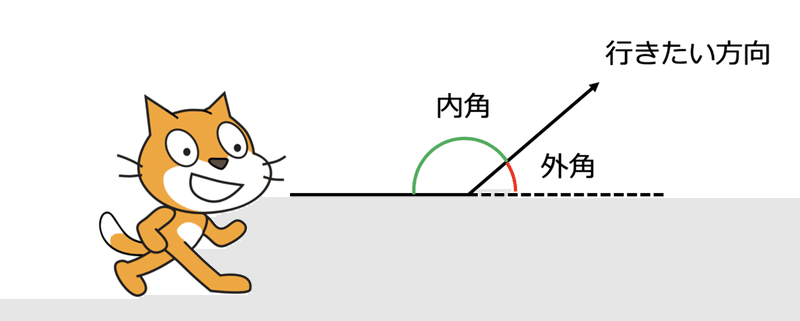
これらを実際にやってみると、外角分だけ曲げればよいのか、内角分だけ曲げればよいのか、というところでつまづきがおこり、スプライトの目線から動かさねばならないことに気がつくのです。
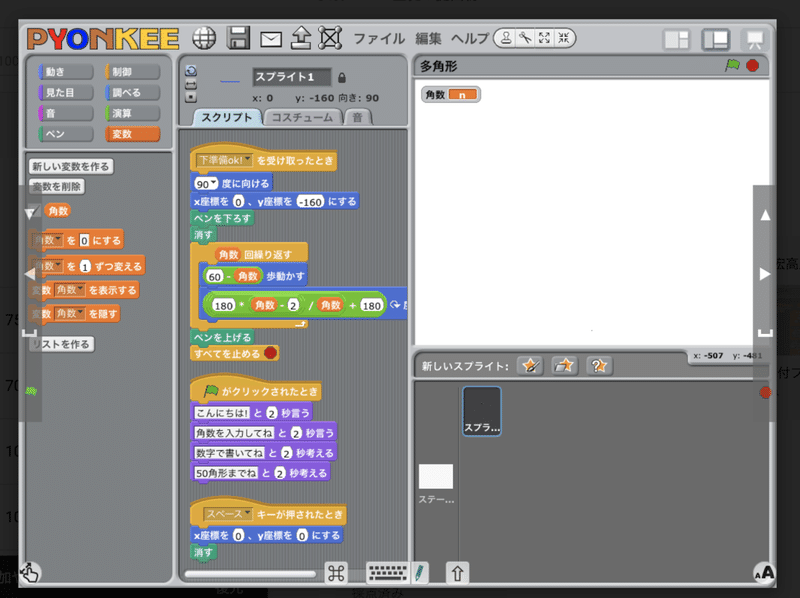
3.どんな正多角形でも描けるようなプログラムを書く
正三角形、正方形、正五角形ときたら、どんな正多角形でも描けるプログラムを書きたくなりますよね!!
ということで、どんな正多角形でも描けるプログラムを考えます。ポイントは「繰り返しを使うこと」です。ステップ1で学んだ表に立ち戻り、右に新しい列を加えて「正n角形の場合にはどうか?」をみんなで考えていきます。
(小学校算数では実際は□や○をつかった式の単元と融合させます)
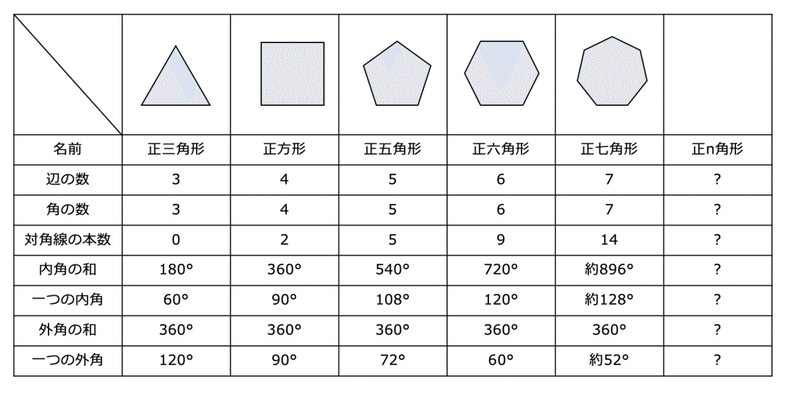
辺の数はnだよね、対角線はどうかな?と、適宜ヒントを与えたり、自分で考えたい子はじっくり考えたり、これかな?と議論をして確かめてみたり。
「帰納的推論」でパターンをnを使って表現し、「演繹的推論」で、実際に当てはまるかどうか試していく。ということを繰り返していくうちに正多角形の書き方を発見してゆきます。
4.パターンブロックを使ってA4用紙を敷き詰めるパターンのある文様をつくる
パターンブロックは様々な図形のブロックを組み合わせて図形を体感的に遊び学ぶことのできるブロックです。
先日紹介したサンフランシスコのエクスプロラトリアムにもパターンブロックがあってびっくり!アメリカでも人気なんですね。

イスラムのアラベスクをイメージして、幾何学模様をうまく敷き詰めていきます。基本的には、正三角形、正六角形を使っていくと作りやすくなります。

パターンがあって美しい模様に仕上がりました。このパターンを次のステップではプログラムで実装します。
5.パターンブロックでつくった文様をプログラムで実装する
ここまでくると、プログラミングのスキルも向上している上に、図形のセンスもだんだんとついてきています。最終的にこの文様をプログラムで実装するためには「どこを1ブロックのかたまりとして繰り返すか」が実装時の最も重要なポイントです。
今回の上の事例で言えば、この模様を作った子どもは、横の一列をワンパターンとしてプログラムを書いていきました。

パターンをプログラムで描くことができました!
ここまでが一連の流れです。今回の学びを改めて振り返ってみると、
1.正多角形を改めて手書きで書いてみて、特徴を分析する
2.プログラムでぶつかる既有知識とのギャップを乗り越える工夫をする
3.規則性を見つけるときにはときに手助けをしてときに議論をして発見につなげる
そんなことが大切であることに気づきます。
プログラミングをする学習は特に算数の分野に入れ込むことができる、というお話があります。正多角形について学ぶときにはプログラミングの抽象化のちからを利用して、正多角形の抽象化の助けとしました。
しかし、全てがプログラミングであったというわけではなく、手を使ったり、コンピュータで行ったり、ブロックを使ったり、様々な操作の中から学ぶことこそが大切だと考えています。
「使いドコロ」こそが、なかなか難しいところ。他にも事例を今後も発信していきたいと思います。
ただ続けることを目的に、毎日更新しております。日々の実践、研究をわかりやすくお伝えできるよう努力します。
