正則化の件

正則化とは？
正則化とは、目的関数にチョコっと付ける可愛い存在です。
どんな時に正則化項を付けるかというと…
■過学習を防ぎたい時
■特徴量選択したい時
とかが挙げられるかなと思います。

正規化項を付ける理由

線形回帰モデルの目的関数は、
𝐿̂ (β)=1/𝑛∑(𝑦–𝑦̂ )^2
です。(※βは回帰係数のことだと思ってください)
つまりこれは、 「予測値 𝑦̂ が真値yと、平均してどれくらいずれているのか」を示します。したがって
1/𝑛∑(𝑦–𝑦̂ )^2=𝐸[(𝑦–𝑦̂ )^2]
とも書けます。　

そしてこの𝐸[(𝑦–𝑦̂ )^2] を分解していきます。
𝐸[(𝑦–𝑦̂ )^2]=𝐸[𝑦^2–2・𝑦・𝑦̂ +𝑦̂ ^2]
=𝐸[𝑦^2]–2𝑦𝐸[𝑦̂ ]+𝐸[𝑦̂ ^2]

ここで
𝑉[𝑥]=𝐸[𝑥^2]–(𝐸[𝑥])^2なので

𝐸[𝑦^2]–2𝑦𝐸[𝑦̂ ]+𝐸[𝑦̂ ^2]
=𝑉[𝑦]+(𝐸[𝑦])^2+𝑉[𝑦̂ ]+(𝐸[𝑦̂ ])^2–2𝑦𝐸[𝑦̂ ]
=𝑉[𝑦]+𝑉[𝑦̂ ]+((𝐸[𝑦])^2−2𝑦𝐸[𝑦̂ ]+(𝐸[𝑦̂ ])^2)
=𝑉[𝑦]+𝑉[𝑦̂ ]+(𝑦–𝐸[𝑦̂ ])^2
となります。

𝑉[𝑦] ：実測値yそのものが持つばらつき
𝑉[𝑦̂ ] ：予測値の平均値周辺のばらつき（バイアス ）
(𝑦–𝐸[𝑦̂ ])^2：予測値の平均が真値に対してどれぐらい離れているか（バリアンス ）
を意味しています。

つまりより良いモデルを作成するためには、
𝑉[𝑦̂ ] ：予測値の平均値周辺のばらつき（バイアス ）
と
(𝑦–𝐸[𝑦̂ ])^2：予測値の平均が真値に対してどれぐらい離れているか（バリアンス ）
を同時に小さくしていく必要があります。

例えば観測データに対して過剰に適合されてしまったモデルの場合は、新規のデータに対するバリアンス（予測値の平均が真値に対してどれぐらい離れているか） が大きくなってしまう傾向にあります。そしてデータ数Nが少なく特徴量pが大きい時は、観測データに対して過剰に適合してしまう恐れがあります。(下図イメージ)

またかなり単純なモデルの場合は、バイアス（予測値の平均値周辺のばらつき）が大きくなる傾向があります。そこで導入するのが正則化項です。
目的関数を𝐿̂ (β)と設定した場合は、観測データに対して過剰に適合してしまう恐れがあるので、回帰係数βに対して制約を付けてあげましょうというのが、正則化とやらです。つまり目的関数にλψ(β)を付け加えた、𝐿̂ (β)+λψ(β)を最小化しようということです。

Ridge

目的関数を𝐿̂ (β)+λψ(θ)にすると記載しました。
ここでλψ(β)をλ|β|^2とした時を、Ridge推定といいます。

λ>0 のとき，Ridge 推定量は

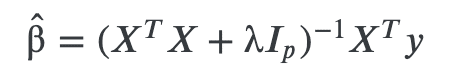
となります。

なぜかと言われれば…

したがってλが大きければ、(𝑋𝑇𝑋+λ)−1の固有値が極端に大きくなることはなく、バイアス（予測値の平均値周辺のばらつき）を抑えることができます。
Ridgeは安定した推定ができますが、回帰係数自体が0に近くなれど0にはなりません。過学習を防ぐという面では有効ですが、特徴量選択という面では有効ではないです。そこで出てくるのがLASSO推定です。

LASSO

LASSOは正則化項をλ|β|とした𝐿̂ (β)+λ|β|を最小化します。
このλ|β|=λ∑|β𝑖|、つまり「絶対値の和」を用いることにより、回帰係数の幾つかを正確に0 と推定できます。
ここでよく出てくる図で、回帰係数が0となるイメージをつかんでおきます。

Why does L1 regularization induce sparse models?

Many illustrate this using the least squares problem with a norm constraint. The least squares level sets are drawn next to the different unit "circles".

I prepared a cool animation which I believe makes it even clearer 🙂 pic.twitter.com/LGcFcm8BOt

— Itay (@itayevron) November 16, 2020

ちなみにLASSO推定は、絶対値を用いているため、Ridge推定のような微分してから推定方程式を解くみたいなことはできません。。。(悲しい)
そのため回帰係数は解析的に求めることができず、数値的に求める方法が提案されているみたい。(座標降下法など)

LASSOは「過学習を防ぐ」、「特徴量選択を可能」にするというメリットがあります。

一方で、「相関の高い変数群で1つしか特徴量を選択しない」かつ「Lassoは選ばれた特徴量が“真に重要な特徴量”であることが保証されない（下記リンク参照）」というデメリットがあります。

タイトル未設定

(もう一つのデメリットとして、特徴量p > データ数Nの時、特徴量が高々N個しか選択されないというのもありますが、今回は触れないです。)

最後に
何か間違っていたら、教えてください。
よろしくお願いします。

参考：

タイトル未設定

タイトル未設定