
宮城県|公立高校入試確率問題2024
1から6までの目が出るさいころが1つあります。
このさいころを2回投げて、1回目に出た目の数を$${a}$$、2回目に出た目の数を$${a}$$とするとき、次の(1)、(2)の問いに答えなさい。ただし、さいころは、どの目が出ることも同様に確からしいものとします。
(1) $${a+b=6}$$が成り立つ確率を求めなさい。
(2) $${\dfrac{b+1}{a}}$$が成り立つ確率を求めなさい。
分類:8 さいころ2つ-和が○以上(以下・未満)
12 さいころ2つ-代入(その1)
(1)文字式を使っていますが
さいころ2回なので表をかいて考えるのがよさそうですね。
問題文では文字を使って$${a+b=6}$$と書いてありますが,つまるところ,2回のさいころの目の数の和が6になるとき,ということです。当てはまるのは,表の次の通り。

このくらいなら,表をかかなくても,1+5,2+4,3+3,4+2,5+1の5通りと列挙できるでしょうか。
(2)は実際に表を埋めてみましょう
(2)は,いくつかアプローチがありそうですが,まずはあまりごちゃごちゃ考えずに表をかいて実際に$${\dfrac{b+1}{a}}$$の値を埋めてみましょう。
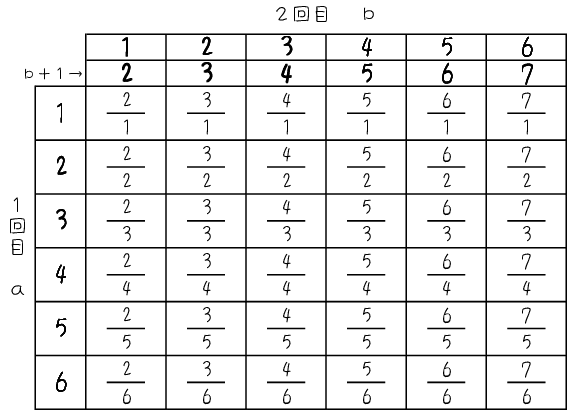
すると,整数になるのは

14通りあることがわかりますので,その確率を求めると$${\dfrac{14}{36}=\dfrac{7}{18}}$$となります。
答
(1)$${\bm{\dfrac{5}{36}}}$$ (2)$${\bm{\dfrac{7}{18}}}$$
(2)を表じゃなく列挙
「$${\dfrac{b+1}{a}}$$が整数である」ということは,「$${b+1}$$が$${a}$$の倍数である」ということですので,分数を持ち出さなくても,こっちの条件で列挙してみてもよいでしょう。
$${b+1}$$の値は,2,3,4,5,6,7の6つのいずれかですので,
●$${a}$$=1のとき,$${a}$$の倍数($${b+1}$$)となるのは 2,3,4,5,6,7 の6通り
●$${a}$$=2のとき,$${a}$$の倍数($${b+1}$$)となるのは 2,4,6 の3通り
●$${a}$$=3のとき,$${a}$$の倍数($${b+1}$$)となるのは 3,6 の2通り
●$${a}$$=4のとき,$${a}$$の倍数($${b+1}$$)となるのは 4 の1通り
●$${a}$$=5のとき,$${a}$$の倍数($${b+1}$$)となるのは 5 の1通り
●$${a}$$=6のとき,$${a}$$の倍数($${b+1}$$)となるのは 6 の1通り
あわせて14通り,というわけです。
この記事が気に入ったらサポートをしてみませんか?
