
基礎編25.5 【研究】5枚のうち3枚を同時に選ぶ
袋の中に1から5までの数字が1つずつ書かれた5個の玉が入っている。この袋から玉を同時に3個取り出すとき,取り出した3個の玉に書かれた数の和が,袋の中に残った2個の玉に書かれた数の積より小さくなる確率を求めなさい。(愛知県2013B)
問題を解く前に・・・
最初に断っておくと、これは「知っておくと便利」なテクニックであって、「知っておかないといけない」テクニック、というわけではありません。
で、この問題のテクニックとしては「分母の出し方をけちる」、偶然を3つ起こすので樹形図…と思いきや「じゃない方」を考えると、偶然2つ起こしたことと同じで、そうすると表ですんじゃう、という省エネテクニックです。(ただし、最後に注意しますが、いつも使えるテクニック、ということではありませんので、あてはまるときは「来た来た、ラッキー」ぐらいに思っておいてほしいやつです)
まじめに解くと・・・
樹形図はこうなります。(詳しくは基礎編25。同じです)

なので分母は10。
このうち、条件を考えると、取り出した方と残った方両方考えるので、残った方もリストアップしておきましょう。

で。それぞれの和と積を考えて、和の方が積よりも小さい場合は・・・

4通り。なので、4/10=2/5
2/5
「じゃない方」を考えると、表が書ける
ところが。何かと樹形図は使いづらいとぶつくさ言ってきている身としては、樹形図じゃなくて表で何とか済ませられないか、と考えているわけです。そうすると、実は「5個のうち3個を同時に取り出す」ことは、「5個のうち残る2個を選ぶ」ことと同じことでは・・・? 見方を変えると、何と「5個のうち3個を同時に取り出す」問題は、「5個のうち2個を同時に取り出す問題」と全く同じ、ってことです。
まどろっこしいかも知れませんが,逆のことを考えてみましょう。「5個のうち(使わない)2個を同時に取り出す」ってことにしたら、・・・ そう、「残った3個を(使うものとして)選んだ」ことになりませんか?
3個同時に取り出すことは、残す2個を決めること同じになります。そして「5個のうち2個を同時に取り出す問題」は基礎編15でやりました。
なので、表が書けちゃうわけです。この考え方を持っていると、速く解けることがあります。

「残り物2つの表」で解いた時の分子は・・・
〔1-2〕のマスは、1と2が残って、3,4,5が取り出された、と考えることにしましょう。そうすると、取り出した3個を上の段、残った2個を下の段に書いておくと、各マスはこんな感じになります。
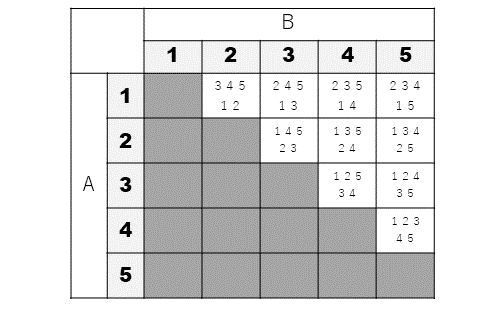
で、問題文のように、取り出した3個の和と、残った2個の積をそれぞれのマスについて計算することにしましょう。

というわけで求める確率は4/10=2/5というわけです。
問題を解いた後に
樹形図や辞書式配列を書いていくのと「あ、じゃない方を考えると表で行ける!」と考えついて、条件を読み替えるのとどっちが楽か、という感じですね。
ポイントとしては、考えることを少なくできる方が、計算は楽になるし、ミスも少なく防ぐことができます。
「▲個から●個同時にとりだす」場合の数は、「▲個から(●個同時に取り出して)残った■個」の場合の数とと同じ・・・ということは、上を目指す人は知っておくとよいテクニックかも知れません。(ただし、気をつけてほしいのは、「5枚のうち3枚、6個のうち4個・・・」のように、残るのが2個・2枚のとき、それから「同時に取り出すとき」ですよ。単純に公式として覚えて、実際に使うときにワケわからなくなることはよくあります。テクニックにおぼれすぎないように。)
-----------------------
<前の問題 次の問題>
問題一覧
この記事が気に入ったらサポートをしてみませんか?
