大学入試センター試験　2018　本試｜大学入試問題なのに中学確率で解ける問題

　大小２個のさいころを同時に投げるとき，「大きいさいころについて，４の目が出る」確率は［　①　］，「２個のさいころの出た目の和が７である」確率は［　②　］，「２個のさいころの出た目の和が９である」確率は［　③　］である。

大学入試センター試験　2018　本試　数学IA　【３】（１）太字部分改題

分類：１　偶然１回の確率　　７　和が○

　さいころ２つですので、表をかきます。①が〇、②が✓、③が☆で、それぞれ条件に合うところを印をつけます。

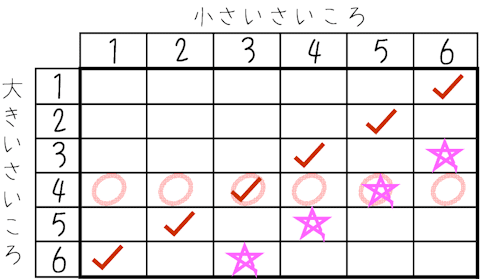
　①は、実は小さいさいころは関係ないので、大きいさいころだけで考えて、実はもう$${\bm{\dfrac{1}{6}}}$$瞬答でもいいですね。
　②・③も、表から$${\dfrac{6}{36}=\bm{\dfrac{1}{6}}}$$、$${\dfrac{4}{36}=\bm{\dfrac{1}{9}}}$$でおしまいです。

答

①$${\bm{\dfrac{1}{6}}}$$　②$${\bm{\dfrac{1}{6}}}$$　③$${\bm{\dfrac{1}{9}}}$$（配点各２点）

でもでもでもでも

　想像の通り、センター試験で出題されている問題文はこんな簡単ではない。

　一般に，事象$${\mathrm{A}}$$の確率を$${P\mathrm{(A)}}$$で表す．また，事象$${\mathrm{A}}$$の余事象を$${\mathrm{\bar{A}}}$$と表す．
　大小２個のさいころを同時に投げる試行において
　　$${\mathrm{A}}$$を「大きいさいころについて，４の目が出る」という事象
　　$${\mathrm{B}}$$を「２個のさいころの出た目の和が７である」という事象
　　$${\mathrm{C}}$$を「２個のさいころの出たロの和が９である」という事象
とする.
　事象$${\mathrm{A}}$$，$${\mathrm{B}}$$，$${\mathrm{C}}$$
の確率は，それぞれ
　　$${P\mathrm{(A)}}$$=［　　］　　$${P\mathrm{(B)}}$$=［　　］　　$${P\mathrm{(C)}}$$=［　　］
である.

大学入試センター試験　2018　本試　数学IA　【３】（１）

　事象という言葉を知っていれば、あとは解き方は中学生、という話。