
新潟県|公立高校入試確率問題2023
1から6までの目のついた1つのさいころを2回投げるとき,1回目に出る目の数を$${a}$$,2回目に出る目の数を$${b}$$とする。このとき,$${\dfrac{24}{a+b}}$$が整数になる確率を求めなさい。
分類: 基礎11 代入(その1)
表で考えましょう
判定する材料が分数です。判定材料を表の枠の中に書くということでやっていくことにするのであれば、ちょっと表を大きめに書いておきましょう。
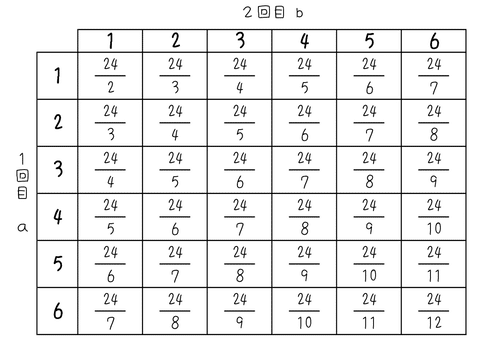
というわけで、約分すると分子が1、整数になるものに印をつけると

となるので、当てはまる場合は17通り。確率は$${\bm{\dfrac{17}{36}}}$$。数え漏らし・数えすぎなど、ちょっと不安になる値ですが、これが正解です。
答
$${\bm{\dfrac{17}{36}}}$$
問題を解いた後に
・・・ということはで考える。
$${\dfrac{24}{a+b}}$$が整数になるということは、$${a+b}$$が24の約数になればよいということです。ということは、$${a+b}$$の値が1,2,3,4,6,8,12,24のどれかになればよい、ということです。表に$${a+b}$$の値だけをかいて、これらのどれかになるところに〇をつけていけば、$${\dfrac{24}{a+b}}$$が整数になる場合を数え上げることができる、というわけです。こっちの方が、表もすっきりしていいですね。

この記事が気に入ったらサポートをしてみませんか?
