福島県｜公立高校入試確率問題2024

　下の図のように，正六角形があり，１つの頂点をＡとする。１から６までの目がある大小２つのさいころを同時に１回投げて，次の〈操作〉を行う。
　ただし，それぞれのさいころについて，どの目が出ることも同様に確からしいものとする。
〈操作〉
・　Ａを出発して，大きいさいころの出た目の数だけ反時計回りに頂点を移動し，とまった位置をＰとする。
・　Ａを出発して，小さいさいころの出た目の数だけ時計回りに頂点を移動し，とまった位置をＱとする。
　例えば，大きいさいころの出た目の数が２で，小さいさいころの出た目の数が３であるとき，例のようになる。

①　ＰとＱが同じ位置になる確率を求めなさい。
②　３点Ａ，Ｐ，Ｑを結んだ図形が二等辺三角形になる確率を求めなさい。

分類：①　応用❷　動かす②　循環型
②　融合Ｂ１（中１・中２図形範囲）

①は６つの頂点の位置を表に

　まず，とまった位置を「ここにとまった！」と呼べるように，六角形の各頂点にそれぞれ次のように名前をつけておくことにします。

　で，表をかくわけですが，大小のさいころの目によってとまる位置は次の通りになります。（時計回り・反時計回りに注意）

　同じ位置に来たところに〇印をつけておきましょう。

　起こりうるすべての場合３６通りのうち，当てはまるのは６通りですから，求める確率は$${\dfrac{6}{36}=\dfrac{1}{6}}$$。

②正三角形も二等辺三角形

　二等辺三角形ができるところに✓印をつけておきます。

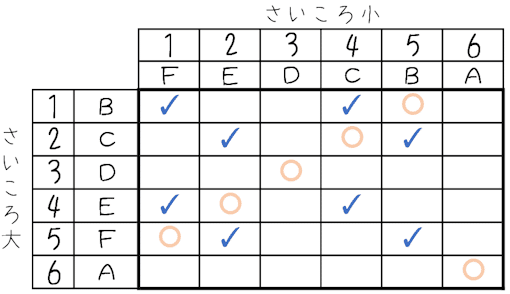
　１つ一つ調べてもよいです。が，さっき〇印が入ったマスの場合は三角形はできないので除外できます。また，６の目が出た場合は大・小どちらもＡに止まりますので，この場合も三角形はできません。まだ，どちらかがＤの位置にとまっていれば，もう一つの頂点で二等辺三角形はつくれないのも気づきましたか？　まあ，これは１つ１つ調べた後の結果論かもしれませんね。

　それぞれのマスの数が，起こりうるすべての場合ということですので，８通りありますので，求める確率は　$${\dfrac{8}{36}=\dfrac{2}{9}}$$。

答

①　$${\bm{\dfrac{1}{6}}}$$　　②　$${\bm{\dfrac{2}{9}}}$$