神奈川県-追検査｜公立高校入試確率問題2022

　右の図１のように，１から１３までの整数が１つずつ書かれた１３枚のカードがある。
　大，小２つのさいころを同時に１回投げ，大きいさいころの出た目の数を$${a}$$，小さいさいころの出た目の数を$${b}$$とする。出た目の数によって，次の【ルール】にしたがってカードを取り除き，残ったカードの枚数について考える。

【ルール】
・$${a=b}$$のとき，$${a}$$以上の素数が書かれたカードをすべて取り除く。
・$${a<b}$$のとき，$${(a+b)}$$以上の偶数が書かれたカードをすべて取り除く。
・$${a>b}$$のとき，$${b}$$以上の奇数が書かれたカードをすべて取り除く。

-----　例　-----
　大きいさいころの出た目の数が３，小さいさいころの出た目の数が５のとき，$${a}$$＝３，$${b}$$＝５だから，$${a<b}$$となり，【ルール】により８以上の偶数が書かれた[８]と[１０]と[１２]のカードを取り除く。
　この結果，図２のように，残ったカードの枚数は１０枚となる。

　いま，図１の状態で，大，小２つのさいころを同時に１回投げるとき，次の問いに答えなさい。ただし，大，小２つのさいころはともに，１から６までのどの目が出ることも同様に確からしいものとする。（マークシート形式から改題）

（ア）残ったカードの枚数が１１枚となる確率を求めなさい。

（イ）残ったカードの枚数が７枚となる確率を求めなさい。

分類：❸（裏返す、取り除く）

アプローチ１　素直にさいころ２個だから表

　偶然は大・小２個のさいころで起こりますので、表をかきましょう。
　そして、さいころとは別の１３枚のカードを操作しますので、表の各マスに何をかくか、ということを考える、ということになります。

　ルールをみる通り、$${a=b}$$、$${a<b}$$、$${a>b}$$の３つの場合がありますので、それぞれに①・②・③と名前をつけて、それぞれの場合ごとに考えることにしましょう。

　①は対角線にあたる部分です。$${a}$$以上（で13以下）の素数が書かれたカードを取り除きます。表に取り除くカードをかいておくことにします。

　②は右上の部分です。$${(a+b)}$$以上（で13以下）の偶数ですから、いったん$${(a+b)}$$をかいてから考えた方がいいかもしれません。

　③は左下の部分、$${b}$$以上（で13以下）の奇数を書き入れます。②と条件が対照的にはなっていないので、注意を。

　（ア）・（イ）の問題文を読むと「残ったカードの枚数」が最終的な判断条件となりますが、「何のカードを取り除いたか→取り除くカードの枚数」を数えれば自動的に残ったカードの枚数も出てきます。念のため、取り除いたカードの枚数をあらためて表にしておいてもいいでしょう。（残ったカードの枚数の方を表にしてもいいですが、ちょっと混乱するかもしれませんね。数えた数をそのまま書き入れる方がいいような気がします）

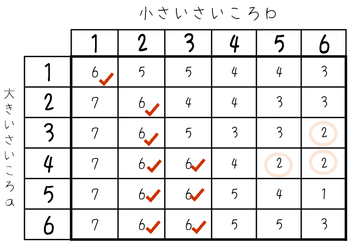
　（ア）は、残ったカードの枚数が１１枚ですから、取り除いたカードが2枚のとき、〇をつけたところが当てはまります。3通りですから、確率は$${\dfrac{3}{36}=\bm{\dfrac{1}{12}}}$$となりますね。

　（イ）は、残ったカードの枚数が7枚、つまり取り除いたカードは6枚です。✓印を数えると9通りありますから、その確率は$${\dfrac{9}{36}=\bm{\dfrac{1}{4}}}$$

答

（１）$${\bm{\dfrac{1}{12}}}$$　　　（２）$${\bm{\dfrac{1}{4}}}$$

問題を解いた後に・・・

アプローチ２　・・・ということは？　で考える？

　アプローチ１で書いたように、「残ったカードの枚数　←　取り除いたカードの枚数　←　何のカードを取り除いたか」のようにさかのぼって考えればいいわけですから、①・②・③のそれぞれのルールが適用される場合について、「（ア）２枚取り除く場合」と「（イ）６枚取り除く場合」がどれだけあるかを考える、というふうに「さかのぼって」考えると、別の場合を考えなくてもいいので、もう少しスマートな解き方になります。
（※ただし、もう少し正確に気を付けて言うと、①・②・③が同時に起こらないので場合分けをして、場合分けしたものをあとでたし算すればよい、という考え方が可能だから、この考え方をしてもよいということです。「①・②・③が同時に起こらないので」というチェックの仕方は高校範囲で学習する内容ですので、その意味で、アプローチ２は、中学範囲を超えた解き方といわざるを得ないのですが・・・）

①：$${a=b}$$　の場合

（ア）２枚取り除く　⇔　[１３]と[１１]の２枚を取り除く　⇔　$${a}$$と$${b}$$が１０か１１の場合　⇔　そんな場合はありえない

（イ）６枚取り除く　⇔　[１３]と[１１]と[７]と[５]と[３]と[２]の６枚をとる　⇔　$${a}$$と$${b}$$が２か１の場合の２通り

②：$${a<b}$$　の場合

（ア）２枚取り除く　⇔　[１２]と[１０]の２枚を取り除く　⇔　$${a+b}$$が９か１０の場合　⇔　$${a+b}$$が９になるのは$${(a,b)=(3,6),(4,5)}$$、$${a+b}$$が１０になるのは$${(a,b)=(4,6)}$$の３通り

（イ）６枚取り除く　⇔　[１２]と[１０]と[８]と[６]と[４]と[２]の６枚をとる　⇔　$${a+b}$$が１か２の場合　⇔　そんな場合はありえない

③：$${a>b}$$　の場合

（ア）２枚取り除く　⇔　[１３]と[１１]の２枚を取り除く　⇔　$${b}$$が１１か１０の場合　⇔　そんな場合はありえない

（イ）６枚取り除く　⇔　[１３]と[１１]と[９]と[７]と[５]と[３]の６枚をとる　⇔　$${b}$$が３か２の場合　⇔　$${(a,b)=(4,3),(5,3),(6,3),(3,2),(4,2),(5,2),(6,2)}$$の７通り

（ア）をまとめると

　残ったカードの枚数が１１枚となる場合は、０＋３＋０＝３で、あわせて３通り。その確率は$${\dfrac{3}{36}=\bm{\dfrac{1}{12}}}$$

（イ）をまとめると

　残ったカードの枚数が７枚となる場合は、２＋０＋７＝９で、あわせて９通り。その確率は$${\dfrac{9}{36}=\bm{\dfrac{1}{4}}}$$