神奈川県-追検査｜公立高校入試確率問題2020

　右の図１のような，３つの袋$${a,b,c}$$がある。
　袋$${a}$$の中には，２，３，５，６の数が１つずつ書かれた４枚のカードが入っている。袋$${b}$$の中には，１，５，６の数が１つずつ書かれた３枚のカードが入っている。袋$${c}$$の中には，３，４，５の数が１つずつ書かれた３枚のカードが入っている。
　Ａさんは袋$${a}$$から，Ｂさんは袋$${b}$$から，Ｃさんは袋$${c}$$から同時にそれぞれ１枚ずつカードを取り出し，３人は次の【ルール】で勝負をする。

【ルール】
３人が取り出したカードに書かれている数の大きさを比べる。
・最も大きい数のカードを取り出した人が１人だけの場合は，その人を勝者とする。
・最も大きい数のカードを取り出した人が１人だけではない場合は，引き分けとする。

例
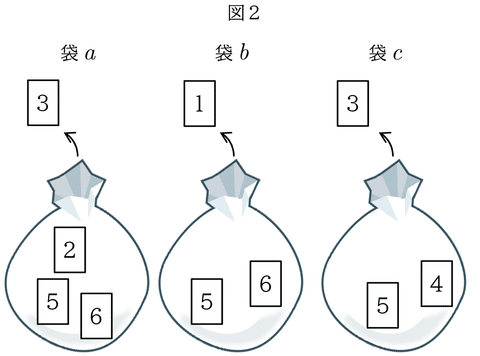
　図２のように，Ａさんが袋$${a}$$から３と書かれたカードを取り出し，Ｂさんが袋$${b}$$から１と書かれたカードを取り出し，Ｃさんが袋$${c}$$から３と書かれたカードを取り出した。
　このとき，最も大きい数は３で，３と書かれたカードを取り出した人はＡさんとＣさんの２人であり，最も大きい数のカードを取り出した人が１人だけではないので，勝負は引き分けとなる。

　いま，図１の状態で，Ａさん，Ｂさん，Ｃさんの３人が袋$${a,b,c}$$から同時にそれぞれ１枚ずつカードを取り出すとき，次の問いに答えなさい。ただし，袋$${a,b,c}$$それぞれについて，袋の中からどのカードが取り出されることも同様に確からしいものとする。

（ア）３人が取り出したカードに書かれている最も大きい数が６で，勝負が引き分けとなる確率を求めなさい。

（イ）Ｂさんが勝者となる確率を求めなさい。

分類：２３：コイン以外のお互いに影響しない３つ以上の偶然

すべての場合をあげられる図表は・・・

　偶然は３つ起こりますから、樹形図をかいて考えることにします。

　起こりうる場合は全部で３６通りで、どの場合が起こることも同様に確からしいです。

（１）は結局・・・

　このうち「最も大きい数が６」となるのは✓の場合で、そのうち「勝負が引き分け」つまり「６を取り出した人が１人だけではない」のは〇の場合ですので、３通りです。したがって、求める確率は$${\dfrac{3}{36}=\bm{\dfrac{1}{12}}}$$となります。

（２）は地道に・・・

　今度はＢさんが勝者になる場合を見つけてみましょう。★印をつけます。

　１３通りですから、確率を求めると$${\bm{\dfrac{13}{36}}}$$。

答

（ア）$${\bm{\dfrac{1}{12}}}$$　　（イ）$${\bm{\dfrac{13}{36}}}$$