
佐賀県|公立高校入試確率問題2024
[S]、[A]、[G]、[A]、[2]、[0]、[2]、[4]と書かれた合計8枚のカードがある。
アルファベットが書かれたカード4枚([S]、[A]、[G]、[A])は【図1】のようにこの順に机の上に並べ、数字が書かれたカード4枚([2]、[0]、[2]、[4])は【図2】のように袋の中に入れる。


下の【操作】を2回行うとき、【例】を参考にして、(ア)~(エ)の各問いに答えなさい。ただし、どのカードの取り出し方も同様に確からしいとし、取り出したカードはもとにもどさない。また、【操作】によって回転させたカードはもとにもどさない。
【操作】
① 【図2】の袋の中からカードを1枚取り出す。
② 取り出したカードの数字に従って、以下のようにアルファベットが書かれたカード4枚すべてを回転させる。
・[0]を取り出したとき、時計回りに180°回転させる。
・[2]を取り出したとき、時計回りに90°回転させる。
・[4]を取り出したとき、反時計回りに90°回転させる。
【例】【図1】の状態から

(ア) 【図1】の状態から2回【操作】を行った。取り出したカードが1回目に[2]、2回目に[0]のカードであったとき、アルファベットが書かれたカードの状態として正しいものを、次のア~エの中から1つ選び、記号を書きなさい。

(イ) 2回【操作】を行うとき、1度も[0]のカードを取り出さない確率を求めなさい。
(ウ) 【図1】の状態から2回【操作】を行った後、アルファベットが書かれたカードの状態が下の【図3】の状態となる確率を求めなさい。

(エ) 【図1】の状態から2回【操作】を行うとき、1回目の操作後と2回目の操作後で、アルファベットが書かれたカードの状態が1度も【図4】の状態とならない確率を求めなさい。
に変更

分類:応用8 その他(回転する)
(ア)は数学?
1回目に取り出したカードは[2]ですから,例のとおりでカードは

の状態になります。次に[0]を取り出して,180°回転しますから

となるわけです。例を読み間違えて,[0]が出るので2回目でも自動的に

となる,と勘違いしていないかを確かめる問題,ということになりますでしょうか。わかっている人からすると,逆に「本当にあっているかな?」と疑心暗鬼になるかも。
(イ)は表をかいて
確率を求めるためにまず,下ごしらえとして,袋からカードを取り出したときに,どのことがらが起こることも同様に確からしいようにするため,2枚の[2]のカードに区別をつけておきます。具体的に1枚を[2],もう一枚を[②]としておきましょう。
そうして,起こりうるすべての場合を表をかいて考えます。[0]をひいた後,もとに戻しませんので,もう一度[0]をひくということはありません。ほかのカードも同様ですので,対角線上のマスは消します。
取り出す順序は関係ありそうなので,それ以上表をいじらないことにします。

すると,起こりうるすべての場合は12通り,ということになります。2回とも[0]のカード以外を取り出す場合を考えればよいですので

6通りで,その確率を求めると$${\dfrac{6}{12}=\dfrac{1}{2}}$$となります。
(ウ)も表をかいて
各マス目に2回目の操作が終わった後の様子を書いて数えたいのですが,SAGAの4文字書くのは面倒なのと,頭文字のSは180°回転したものと見分けがつきにくいので,Aの文字を回転させたものをかくことにしておきます。いったん,1回目の操作が終わった後のAを左側に書いておいて考えるとわかりやすいかもしれません。

これで表を埋めておきましょう。
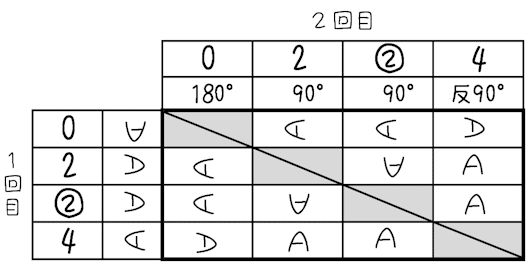

の状態になっているのは

4通りですから,求める確率は$${\dfrac{4}{12}=\dfrac{1}{3}}$$となります。
(4)も表から
1回目でも2回目でも逆さにならないように,ということですので,まず1回目が逆さになる場合を排除しておきましょう。

1回目で逆さにならなかったけど,2回目で逆さになってしまうのは
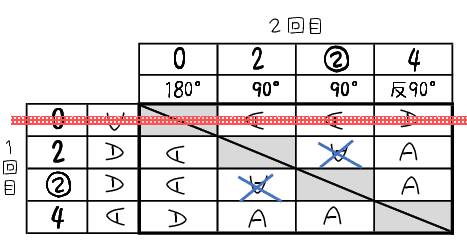
さらに2通りありましたので,残るは7通り。ですから確率は$${\dfrac{7}{12}}$$と求めることができます。
答
(ア)エ (イ)$${\bm{\dfrac{1}{2}}}$$ (ウ)$${\bm{\dfrac{1}{3}}}$$ (エ)$${\bm{\dfrac{7}{12}}}$$
この記事が気に入ったらサポートをしてみませんか?
