
神奈川県|公立高校入試確率問題2020
神奈川県の確率問題は,ここ数年、ここでの分類「応用問題」か「融合問題」の形で出題されています。この年も立体図形(+三平方の定理?)との融合問題。
右の図1のように,正方形ABCDを底面とし,AE=BF=CG=DHを高さとする立方体がある。
また,図2のように,袋Pと袋Qがあり,その中にはそれぞれB,C,D,E,F,Gの文字が1つずつ書かれた6枚のカードが入っている。袋Pと袋Qからそれぞれ1枚ずつカードを取り出し,次の【ルール】にしたがって,図1の立方体の8個の頂点のうちから2個の点を選ぶ。
【ルール】
袋Pと袋Qから取り出したカードに書かれた文字が異なる場合は,それぞれの文字に対応する点を2個の点として選ぶ。
袋Pと袋Qから取り出したカードに書かれた文字が同じ場合は,その文字に対応する点および点Hを2個の点として選ぶ。
いま,図2の状態で,袋Pと袋Qからそれぞれ1枚ずつを取り出すとき,次の問いに答えなさい。ただし,袋Pと袋Qそれぞれについて,袋の中からどのカードが取り出されることも同様に確からしいものとする。
(ア) 選んだ2個の点が,ともに平面ABCD上の点となる確率を求めなさい。(選択肢方式から改題)
(イ) 選んだ2個の点および点Aの3点を結んでできる三角形についてその3つの辺の長さがすべて異なる確率を求めなさい。


偶然2つなので、まずは表をかいてみる
袋Pからも、袋Qからも1枚ずつ、2つの偶然が起こりますので、まずは表をかいてみます。各マスには「選んだ2つの点」を書きます。

(ア)は・・・
2点が平面ABCD上にあると言うことは、結局、選んだ2点がどちらもBかCかDのどれかであること、と同じことですね。
あてはまるのは,次の表のようになります。

求める確率は$${\dfrac{6}{36}=\bm{\dfrac{1}{6}}}$$
(イ)は・・・
実際に、各マスについて確認をしてみましょう。ただし、時間はかかりそうです。
調べるのは・・・
このとき、ポイントなのは,PとQで違うものが出てきたときに「右上」にあるマスト「左下」にあるマスで、同じ三角形となっているものが2つずつできているので、確かめるのはそのうちの一方でよい、ということ。こうすることで、確かめる三角形の数はかなり減ります。
3つの辺の長さを確かめていくと・・・
実際に確かめていくと、次の3種類の「長さ」の辺があることがわかると思います。
① 立方体の1辺と同じもの
②(同じ平面上で)側面の正方形の対角線と同じもの
③(同じ平面上にない)立方体のいちばん遠いところどうしの点を結ぶもの
この3種類で構成されるものであることを意識してチェックすると,次の表のようになります。
(三平方の定理を使って実際長さを求めてもいいのでしょうが、この問題では結局3種類あって、分類できることが大切なので、実際の線分の長さは求めないでおきます)

左下のも、チェックはしていませんが,右上でOK担ったものを数え直すのを忘れないこと。条件を満たしているのは16通りあります。求める確率は、$${\dfrac{16}{36}=\bm{\dfrac{4}{9}}}$$
答
(ア) $${\bm{\dfrac{1}{6}}}$$ (イ) $${\bm{\dfrac{4}{9}}}$$
問題を解いたあとに・・・
もうちょっとスッキリ解けないか? というのは研究してみてもいいかもしれません。
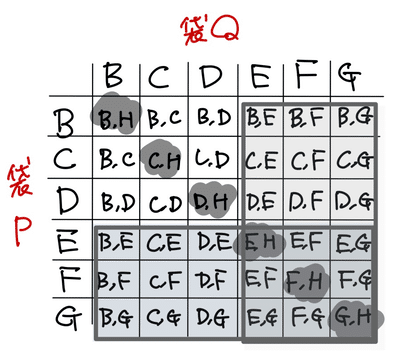
(ア)はPかQで、E・F・Gどれか1つでも出たらアウトなので消す、同じものが出てもHが入ってくるとアウト、ということで考えると、つぎの6つしか残らない,と考えてもよいでしょう。
(イ)は,上に書いた①・②・③での組み合わせ、というアプローチで行くと、③にあてはまるのはAG・BH・FD・ECの4つしかないので,ここから絞っていくといいかもしれません。
●AGを使う場合
もう1点がB・C・D・E・F・Hどの場合でも条件に合います。
ですから、選ばれる2点がBG・CG・DG・EG・FG・HGいずれの場合もOKということになります。(BG・CG・DG・EG・FGは各2通り、HGはPからもQからもGをひく1通りで、合わせて11通り。)
●BHを使う場合
条件に合っています。ですから、選ばれる2点がBBの場合はOKということになります。(両方からBを取り出す1通り)
●FDを使う場合
条件に合っています。ですから、選ばれる2点がFDの場合はOKということになります。(2通り)
●ECを使う場合
条件に合っています。ですから、選ばれる2点がECの場合はOKということになります。(2通り)
というわけで、合わせて16通りということになります。PとQで同じものをひいたときの扱いが,ちょっと問題を複雑にしていることもわかりますね。
この記事が気に入ったらサポートをしてみませんか?
