
鹿児島県|公立高校入試確率問題2023
下の図で,放物線は関数$${y=\dfrac{1}{4}x^2}$$のグラフであり,点Oは原点である。点Aは放物上の点で,その$${x}$$座標は4である。点Bは$${x}$$軸上を動く点で,その$${x}$$座標は負の数である。2点A,Bを通る直線と放物線との交点のうちAと異なる点をCとする。点Cの$${x}$$座標がー2であるとき,次の問いに答えなさい。

(1) 点Aの$${y}$$座標を求めよ。
(2) 点Bの座標を求めよ。ただし,求め方や計算過程も書くこと。
(3) 大小2個のきいころを同時に投げ,大きいさいころの出た目の数を$${a}$$,小さいさいころの出た目の数を$${b}$$とするとき,座標が($${a}$$ー2,$${b}$$-1)である点をPとする。点Pが3点O,A,Bを頂点とする△OABの辺上にある確率を求めよ。ただし,大小2個のさいころはともに,1から6までのどの目が出ることも同様に確からしいものとする。
※(3)の確率に関係する問題だけに改題
分類 融合C3 放物線・双曲線
(1)まずはAの座標を求めよう
まず点Aの座標を求めます。放物線$${y=\dfrac{1}{4}x^2}$$上にあり、$${x}$$座標が4である点を求めればいいので、$${x=4}$$を$${y=\dfrac{1}{4}x^2}$$に代入すればよいでしょう。$${y=\dfrac{1}{4}×4^2=4}$$ですから、点Aの$${y}$$座標は4です。
(2)点Bと点Cの座標を勘違いしないように
点Bはどうでしょう。まずは点Cの座標を求めます。放物線$${y=\dfrac{1}{4}x^2}$$上にあり、$${x}$$座標が-2である点ですので、$${x=-2}$$を$${y=\dfrac{1}{4}x^2}$$に代入すればよいです。$${y=\dfrac{1}{4}×(-2)^2=1}$$ですから、点Cの座標は(-2,1)。直線ACと$${x}$$軸との交点がBですので、次に直線ACの式を求めます。
2点(4,4),(-2,1)を通りますので、グラフの傾きは
$${\dfrac{4-1}{4-(-2)}=\dfrac{3}{6}=\dfrac{1}{2}}$$
したがって、この1次関数は$${y=\dfrac{1}{2}x+b}$$と書くことができます。
グラフが(4,4)を通るので,上の式に,$${x}$$=4,$${y}$$=4を代入すると
$$
\begin{align*}
4&=\dfrac{1}{2}\times4+b\\
&=2+b\\
b &=4-2\\
\bm{b &=2}
\end{align*}
$$
よって、直線ACの式は $${y=\dfrac{1}{2}x+2}$$ です。(連立方程式を立てて求める方法でももちろんオッケーです)
点Bは直線ACと$${x}$$軸との交点ですので、この式に$${y=0}$$を代入して$${x}$$座標を求めると
$$
\begin{align*}
0&=\dfrac{1}{2}\timesx+2\\
\dfrac{1}{2}\timesx&=-2\\
x &=-2\times\dfrac{2}{1}\\
\bm{x &=-4}
\end{align*}
$$
以上のように、点Bの座標は(-4,0)です。
(3)直線上で座標が整数になる点
点Aと点Bの座標を求めることができました。さて、△OABの辺上にある確率を求めることになります。点Pは$${x}$$座標がー1か0か1か2か3か4のどれかで、$${y}$$座標は0か1か2か3か4か5のどれか、ということです。その間で、線分OA上・線分AB上・線分BO上にある点を考えればよいわけです。具体的には次のようになります。
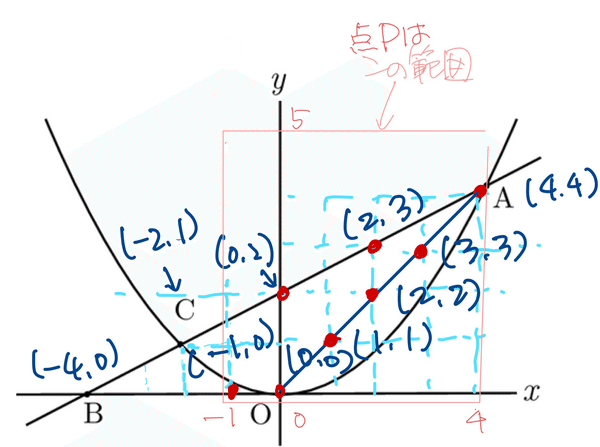
表をかいて、その時の点Pの$${x}$$座標、$${y}$$座標も書き添えておきましょう。
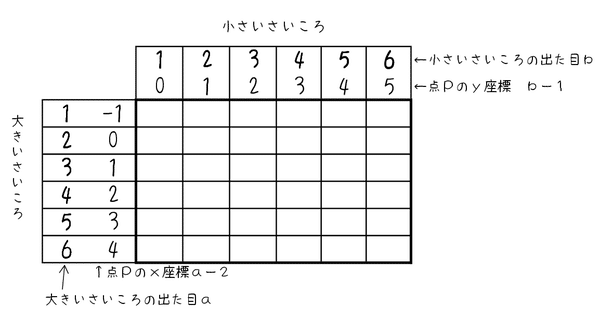
それぞれのマスには、座標が対応しています。意味としてはこういうことです。座標平面とは縦横や上下関係が狂っていますので、要注意。

そのうち、線分OA上か線分AB上か線分BO上にある点に当てはまるのは、〇のところです。

条件に当てはまるのは8通りですので、その確率を求めると$${\dfrac{8}{36}=\bm{\dfrac{2}{9}}}$$
答
(1)4 (2)(-4,0)※求め方・計算は上記。
(3) $${\bm{\dfrac{2}{9}}}$$
この記事が気に入ったらサポートをしてみませんか?
