
福島県|公立高校入試確率問題2020
右の図のように,Aの箱の中には0,1,2,3,4,5の数字が1つずつ書かれた6枚のカードが,Bの箱の中には1,2,3,4,5,6の数字が1つずつ書かれた6枚のカードが入っている
Aの箱の中からカードを1枚取り出しそのカードに書かれた数を$${a}$$とし,Bの箱の中からカードを1枚取り出し,そのカードに書かれた数$${b}$$とする。ただし,どのカードを取り出すことも同様に確からしいものとする。
① 積$${ab}$$が0となる場合は何通りあるか求めなさい。
② $${\sqrt{ab}}$$の値が整数とならない確率を求めなさい。

表を書いて考えます。
偶然は、Aの箱から1枚取り出すことと、Bの箱から1枚取り出すことの2つあります。偶然2つなので、表をかいて考えるといいですね。

すべての場合は36通り。各マスに積$${ab}$$を書いておきましょう。
①は?
上の表から、積が0になるのは6通りです。
②は?
$${\sqrt{ab}}$$の値が整数にならないところに印をつけてみましょう。
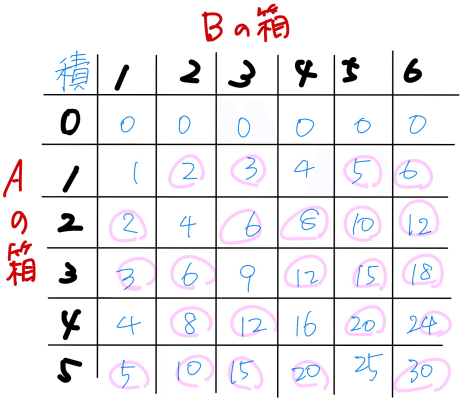
条件にあてはまるのは23通りですので、求める確率は$${\bm{\dfrac{23}{36}}}$$となります。
答
① 6通り $${\bm{\dfrac{23}{36}}}$$
分類 融合問題A2平方根
この記事が気に入ったらサポートをしてみませんか?
