北海道｜公立高校入試確率問題2024

　図１のような頂角が１２０°の二等辺三角形があります。

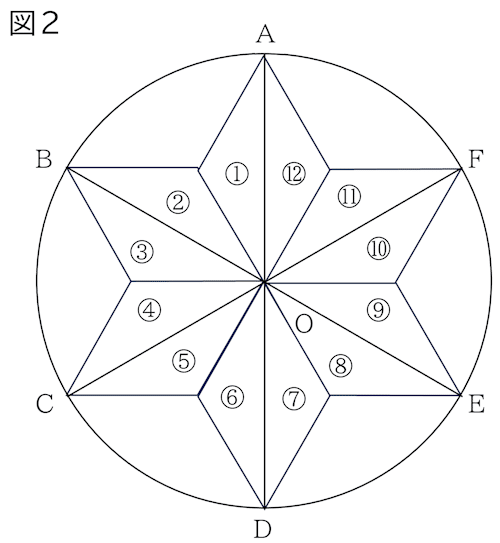
　また，図２のように，円Ｏの円周を６等分する点Ａ，Ｂ，Ｃ，Ｄ，Ｅ，Ｆがあり，図１と合同な二等辺三角形①～⑫を，それぞれの三角形の最も長い辺が円Ｏの半径となるように並べます。

　次の（１），（２）に答えなさい
 
（１）　①を，点Ｏを中心として時計回りに回転移動して，⑨に初めてびったり重なったのは，何度回転移動したときですか。その角度を求めなさい。

（２）　種類の異なる３枚の硬貨Ｘ，Ｙ．Ｚがあります。硬貨Ｘ，Ｙ，Ｚを同時に投げ，表と裏の出かたに応じて，①に，次の[１]～[３]の操作を順に行い，最後に①～⑫のどの三角形に重なるかを調べます。
［１］　硬貨Ｘが表のときは線分ＡＤを対称の軸として対称移動させ，裏のときは移動させない。
［２］　硬貨Ｙが表のときは点Ｏを回転の中心として１８０°回転移動させ，裏のときは移動させない。
［３］　硬貨Ｚが表のときは平行移動してびったりと重なる三角形に移動させ，裏のときは移動させない、
　３枚の硬貨Ｘ，Ｙ，Ｚを同時に投げるとき，①が最後に重なる三角形が⑦となる確率を求めなさい。 

分類：融合Ｂ１　中１・２図形範囲

（１）ちゃんと文章を読もう

　まず図１の三角形のここの角が３０°であることを押さえておきましょう。頂角が１２０ですから，（１８０－１２０）÷２で求めてもいいですし，１周３６０°を１２等分しているので３６０÷１２で求めてもいいですね。

　で，Ｏを回転の中心にっして①を回転移動して⑨に重なるところを探すのですが，①～⑫の番号は「反時計回り」についています。こっちの方向に回転させてしまいそうですが，問題文には「時計回り」と書いてある「ひっかけ」問題。注意が必要です。

　ちゃんと時計回りさせると，３０度を４つ分ですから３０×４で，答えは１２０°。

（２）は樹形図を

　コインがＸ，Ｙ，Ｚの３つありますので，樹形図をかきます。おもてを「お」，うらを「う」と書くことにします。

　それぞれ①だった図形は途中経過でどの図形と重なるか，この図の中に書き入れていきましょう。

　というわけで起こりうるすべての場合の数は８通りで，そのうち⑦と重なるのは２通りですので，求める確率は$${\dfrac{2}{8}=\dfrac{1}{4}}$$。

答

（１）１２０°
（２）$${\bm{\dfrac{1}{4}}}$$