大阪府Ｃ問題｜公立高校入試確率問題2024

　二つの箱Ａ、Ｂがある。箱Ａには奇数の書いてある３枚のカード［１］、［３］、［５］が入っており、箱Ｂには偶数の書いてある３枚のカード［４］、［６］、［８］が入っている。Ａ、Ｂそれぞれの箱から同時にカードを１枚ずつ取り出し、箱Ａの中に残っている２枚のカードに書いてある数の和を$${a}$$、箱Ｂの中に残っている２枚のカードに書いてある数の和を$${b}$$、箱Ａから取り出したカードに書いてある数と箱Ｂから取り出したカードに書いてある数との和を$${c}$$とする。このとき、$${a<c<b}$$である確率はいくらですか。Ａ、Ｂそれぞれの箱において、どのカードが取り出されることも同様に確からしいものとして答えなさい。

分類：１７　お互いに影響しない２つの偶然

どんな表をかきましょう？

　箱Ａから１枚カードを取り出す偶然と，箱Ｂから１枚カードを取り出す偶然の２つのできごとが起こりますので，表をかいて考えることにしましょう。箱Ａで起こる同じ確率（同様に確からしい）ことがらを縦に，箱Ｂで起こる同じ確率（同様に確からしい）ことがらを横に並べた表をつくります。

　$${a}$$と$${b}$$の値はもう計算できますね。

　$${c}$$の値を計算して，各マス目を埋めましょう。

　$${a<c<b}$$を満たす場合は

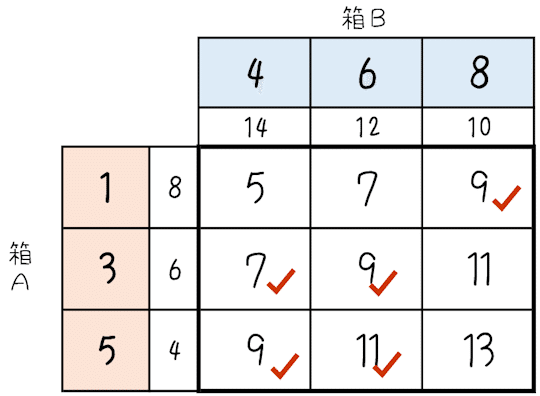
５通りですから，求める確率は$${\dfrac{5}{9}}$$。

答

$${\bm{\dfrac{5}{9}}}$$