大学入試センター試験　2003　追試｜大学入試問題なのに中学確率で解ける問題

（１）　１枚の硬貨を３回投げたとき，表が１回だけ出る確率は［　　］である．
（２）　１枚の硬貨を３回投げたとき，表が少なくとも１回出る確率は［　　］である．
（３）　１枚の硬貨を４回投げたとき，表が続けて２回以上出る確率は［　　］である．

2003　大学入試センター試験　追試 数学I・数学IA共通【1】[2]

（１）は樹形図で

　偶然は３回起こりますので、樹形図をかいて考えます。表を〇、裏を●でかいておきます。

　起こりうるすべての場合を数えると８通り。あとは条件に合う場合を探します。

　３通りです。求める確率は$${\bm{\dfrac{3}{8}}}$$

（２）は「じゃない」方

　分母は（１）同様８。「表が少なくとも１回出る」で、少なくとも１なので、じゃない方から考えた方がよいでしょう。「表が少なくとも１回出る」じゃない、というのは「表が１回も出ない」つまり「３回とも裏」ですので、条件に合うのは１通り。求める確率は
$${1-\dfrac{1}{8}=\dfrac{7}{8}}$$
ですね。

（３）も樹形図かいちゃえ

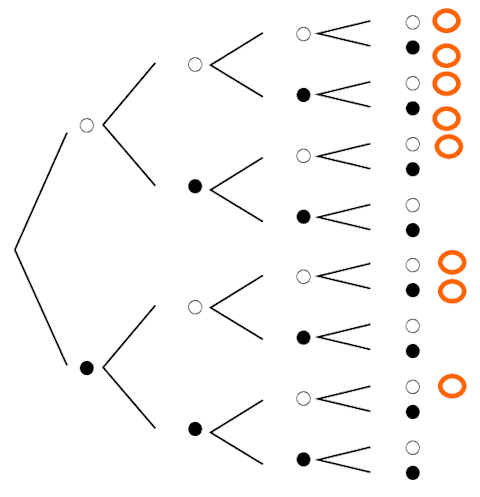
というわけで、起こりうるすべての場合１６通りのうち、表が続けて２回以上出るは８通りですので$${\dfrac{8}{16}=\bm{\dfrac{1}{2}}}$$。

答

(1)$${\bm{\dfrac{3}{8}}}$$（5点）　　(2)$${\bm{\dfrac{7}{8}}}$$（5点） (3)$${\bm{\dfrac{1}{2}}}$$(5点）

　まさしく中学校レベルの問題だけで１００点中１５点ももらえるだなんて！　いい時代でしたね。続けて（４）にも挑戦してしまいましょう。

（４）　１枚の硬貨を５回投げたとき，表が続けて２回以上出ることがない確率は［　　］である．

　$${\bm{\dfrac{13}{32}}}$$ですね。樹形図をしっかりかいて根気よく見つける必要はありますが、ちゃんとできれば、中学生でも解けますし、これで２０点ですよ。ただ、いわゆる「ゆとり時代」で、（２）の「じゃない方」＝余事象の確率は高校で習うことになっていたわけでした。

（４）を樹形図じゃなく解くとしたら？

　さすがに樹形図はつらい？　ならばレベル３の「分母は公式、分子は独自列挙」で解いてみましょう。表が５回中何回出るか、で場合分けします。これも結構な力業。
●表が５回出る場合は、当然「表が続けて２回以上」になっていますので、ダメ
●表が４回出る場合　表４つの間に１つ裏が入っています。つまり　
１表２表３表４表５
の５つの数字の場所のうち、１つに裏が入るわけですが、どこに裏が入っても「表が続けて２回以上」になっています。ダメです。確かめてみると
裏表表表表　表裏表表表　表表裏表表　表表表裏表　表表表表裏
●表が３回出る場合　表が２・１に分かれるとだめですね。つまり条件に合うのは
表裏表裏表
の１通りしかありえません。
●表が２回出る場合　表２回、裏３回の組合せは$${_5  \mathrm{C}_2=10}$$通り。そのうち表が続けて２回になるのは［表表］をひとかたまりと考え、裏３回との４つの組合せと考えて$${_4  \mathrm{C}_1=4}$$通り。かき出すと
表表裏裏裏　　裏表表裏裏　　裏裏表表裏　　裏裏裏表表
ですから、これ以外、ということになりますので、条件に合うのは10-4=６通り。
●表が１回出る場合　表が続けて２回にはなりようがありません。表１回、裏４回の組合せ$${_5  \mathrm{C}_1=5}$$通りはすべてOK。
●表が０回出る場合　これも表が続けて２回にはなりようがありませんが、裏５回の１通りしかありませんね。
全部足すと１＋６＋５＋１＝１３通り、ということになります。