
京都府前期|公立高校入試確率問題2023
あたりくじが2本,はずれくじが2本の合計4本のくじが入った箱がある。この箱から,太郎さん,次郎さん,花子さんが,この順に1本ずつくじをひく。このとき,花子さんだけがあたりくじをひく確率を求めよ。ただし,ひいたくじは箱にもどさず,どのくじがひかれることも同様に確からしいものとする。
分類 24 取り出して戻さず何回も
偶然は3回→樹形図
太郎さん,次郎さん,花子さんがそれぞれ偶然を起こします。偶然は3回起こりますから、樹形図をかいて考えることにします。
4本のくじに、それぞれ1・2・3・4の番号をつけておいて、1・2が当たり、3・4がハズレ、と考えることにしましょう。
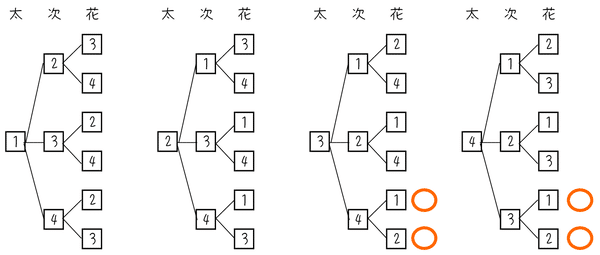
すべての場合は24通りあり、そのどれが起こることも同様に確からしいです。
花子さんだけが当たりくじをひくということは、太郎さん・次郎さんが両方[3]か[4]のどちらかをひいて、花子さんが[1]か[2]をひく場合、ということですから、図の中の〇印のところ。4通りあります。
ですから、その確率は$${\dfrac{4}{24}=\bm{\dfrac{1}{6}}}$$。
答
$${\bm{\dfrac{1}{6}}}$$
問題を解いた後に
(高校での解き方)
太郎がハズレをひく確率 $${\dfrac{2}{4}=\dfrac{1}{2}}$$
太郎がハズレをひいたあと次郎がハズレをひく確率 $${\dfrac{1}{3}}$$
太郎と次郎が両方ハズレをひけば、自動的に花子は当たりになるので、求める確率は $${\dfrac{1}{2}×\dfrac{1}{3}=\dfrac{1}{6}}$$
でもこの解き方を中学生に教えるのはNGですね。
この記事が気に入ったらサポートをしてみませんか?
