
千葉県|公立高校入試確率問題2016
右の図のように,2点A(5,0),B(0,5)があり,線分OA,OBを半径とするおうぎ形OABがある。
大小2つのさいころを同時に1回投げ,大きいさいころの出た目の数を$${a}$$,小さいさいころの出た目の数を$${b}$$として,($${a,b}$$)を座標とする点Pをとる。
このとき,点Pがおうぎ形OABの内部または周上にある確率を求めなさい。
ただし,さいころを投げるとき,1から6までのどの目が出ることも同様に確からしいものとする。

分類:融合《D2》座標平面上の図形-2点の距離
問題用紙の図は方眼がないので・・・
点Pがおうぎ形OABの内部または周上にあるとは?
線分OPの長さは$${\sqrt{a^2+b^2}}$$と表せます。点Pがおうぎ形OABの内部または周上にあるとは、線分OPの長さが0以上5以下であればよい、ということになります。線分OPの長さは$${\sqrt{a^2+b^2}}$$と表せますので、$${\sqrt{a^2+b^2}}$$を調べればよいのですが、平方根があるものは,2乗して考えて、平方根の中身だけで検討すればよいですね。
これは,分数のときに分母が固定されるならば分子だけを見ればよい,というように,数学の問題を解くときにはちょっとしたテクニックとして,身につけておくのがよいですね。
2乗したもの$${a^2+b^2}$$を表にして、0以上25以下の範囲を探してみましょう。どちらかの目が5~6なら、すでに範囲を超えてしまうことは理解できますね。表をかいてみると、条件に当てはまるのは15通り。
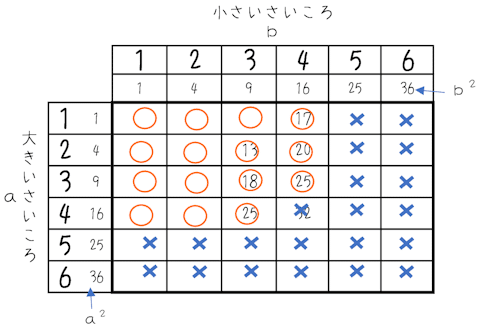
ですから、求める確率は$${\dfrac{15}{36}=\bm{\dfrac{5}{12}}}$$
答
$${\bm{\dfrac{5}{12}}}$$
この記事が気に入ったらサポートをしてみませんか?
