兵庫県｜公立高校入試確率問題2012

　豆電球６個が，図１のように横一列に並べられている。それぞれの豆電球にはスイッチが１個ずつ付いており，そのスイッチを１回押すと点灯し，もう１回押すと消える。
　次の規則にしたがって，操作①から操作③を順に行う。

＜規則＞
操作①　すべての豆電球が消えた状態にする。
操作②　さいころを１回投げ，出た目の数を$${p}$$とし，左から$${p}$$番目までのすべてのスイッチを押す。
操作③　続けてもう１回さいころを投げ，出た目の数を$${q}$$とし，右から$${q}$$番目までのすべてのスイッチを押す。
　操作②で$${p}$$の目，操作③で$${q}$$の目が出たとき，さいころの目の出方を（$${p,q}$$）と表すことにする。
　例えば，さいころの目の出方が，（３，４）のとき，操作①から操作③における６個の豆電球の点灯のしかたは，図２のようになる。

　次の問いに答えなさい。

（１）　さいころの目の出方が（５，３）のとき，操作①から操作③を行ったあと，点灯している豆電球は何個あるか，求めなさい。

（２）　操作①から操作③を行ったあと，左から１番目と２番目，右から１番目の３個だけ豆電球が点灯しているようなさいころの目の出方をすべて求めなさい。ただし，目の出方を（$${p,q}$$）と表して答えなさい。

（３）　操作①から操作③を行ったあと，４個の豆電球が点灯している確率を求めなさい。

（４）　左から３番目の豆電球が切れてスイッチを押しても点灯しないとき，操作①から操作③を行ったあと，４個の豆電球が点灯している確率を求めなさい。

分類：応用〈３〉　裏返す

（１）はやってみよう

　（５，３）のときは、（Ｍはランプがついている、✔は一回ついたけど消えた，を表すとすると」）

というふうになるので、電球がついているのは４個

（２）は１つ１つ・・・

　さいころ１回目で出たもの（$${p}$$）から、２回目で「左から１番目と２番目，右から１番目の３個だけ豆電球が点灯している」状態になるのはどうなるか、１つ１つ考えてみます。

☆$${p}$$＝１のとき　　電球は　○●●●●●　の状態となっています。左側から１つ目がついたまま２つ目の電球をつけるためには２回目$${q}$$＝５である必要がありますが，それだと○○○○○○と電球が全てついてしまいます。

☆$${p}$$＝２のとき　　電球は　○○●●●●　の状態となっています。左側の電球はバッチリです。ここから２回目は$${q}$$＝１だと求められる状態になります。（２，１）

☆$${p}$$＝３のとき　　電球は　○○○●●●　の状態となっています。左側から３つ目の電球を消すためには$${q}$$＝４が必要ですが、その代わり４～６つ目が全てついて○○●○○○となりますので、ダメです。

☆$${p}$$＝４のとき　　電球は　○○○○●●　の状態となっています。左側から３つ目・４つ目の電球を消すためには２回目$${q}$$＝４である必要がありますが，それだと○○●●○○と右側から２つ目の電球もついてしまいますので、やはりダメです。

☆$${p}$$＝５のとき　　電球は　○○○○○●　の状態となっています。左側から３つめ～５つめの電球を消すためには２回目$${q}$$＝４であればよく、それで○○●●●○となりオッケーです。（５，４）

☆$${p}$$＝６のとき　　電球は　○○○○○○　の状態となっています。左側から３～６つ目の電球を消すためには$${q}$$＝４が必要ですが、６つ目も消えて○○●●●●となりますので、ダメです。

（３）は表を書いてしまいましょう。

　この場合はこうで、この場合はこうで・・・と考えてみてもいいですが、（２）をもとに、表を書いてしまって、あとで数える作戦でいってみましょう。

クリックすると拡大します

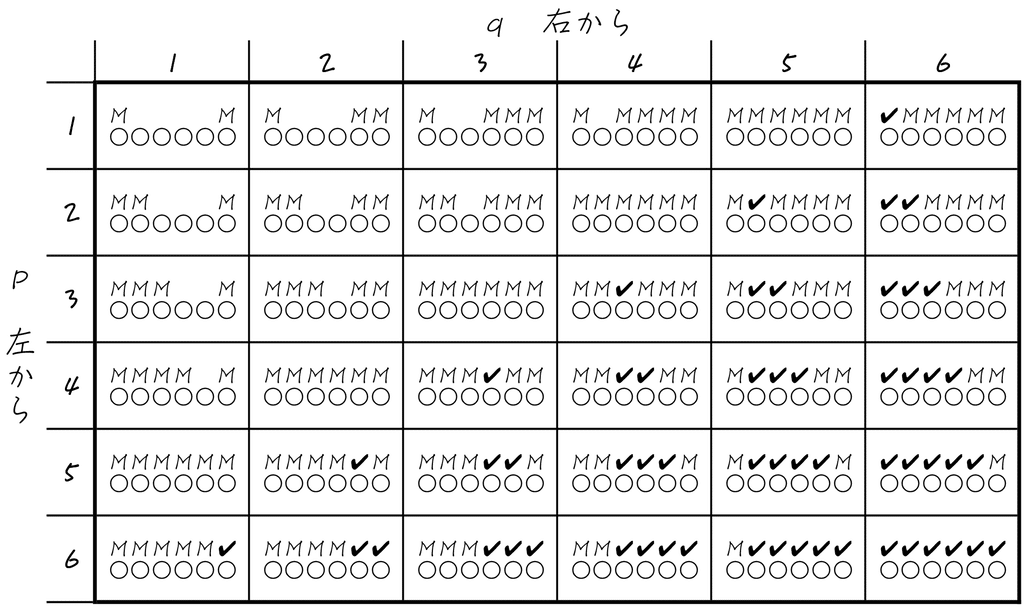
　数えてみると、８通りありますので、確率は$${\dfrac{8}{36}=\bm{\dfrac{2}{9}}}$$です。

（４）も表を使いましょう

　（４）は、３番目の電球が消えていることにして、数え直しましょう。

（３）で数えた４つ電球がついている場合のうち３番がついているものを除外して（∅）、５つ電球がついている場合のうち３番がついているものを加えて（✔）、○と✔印を数え直すと、１２通り。ですから確率を求めると、$${\dfrac{12}{36}=\bm{\dfrac{1}{3}}}$$です。

答

（１）４個　（２）（２，１），（５，４）　（３）$${\bm{\dfrac{2}{9}}}$$  　　（４）$${\bm{\dfrac{1}{3}}}$$