基礎編３　「サイコロ２回の分母①」大小のさいころ２個

　大小２つのさいころを同時に投げるとき，２つとも同じ目が出る確率を求めなさい。（栃木県2019）

問題を解く前に①　なぜ高校入試にサイコロ２つの問題が多い？

　基礎編３～１７は、２つの偶然が起こるときの確率の求め方を考えます。

　高校入試で出される確率の問題の８割は、偶然が２つ起こるやつです。そして、その中でもダントツなのは、大小２つのさいころをつかって２つ偶然を起こす問題です。高校入試問題をつくる人は、どうも２つのさいころが大好きのようです、ダイスだけに。

　中学校で確率を求める問題のしばりとして「図表を使ってすべての場合（分母）が求められる」というのがあります。なので、高校入試の問題を作る人からしても、手軽に適度な難しさの確率の問題が作りやすい、というのがあるのでしょうね。

問題を解く前に②　なぜサイコロ２つは表を書く？

　本題に入る前に、もうひとつ続けます。

　受験参考書なんかでは「２つのさいころは表を書け！」と標語のように書いてあるものがあります。教科書でも、あからさまには書いていませんが、この大小２つのさいころの問題はしれっと表を書いて問題を解きます。

　しかし、なぜ２つのさいころだと表を書くのでしょうか？　その理由を説明しているものは見たことがありません。

　ここで、だれも教えてくれない、その理由を書いてしまうことにしましょう。

　偶然が２つ起こるときは、表で考えるとそこそこ考えやすいからです。

分母は・・・

　大小２つのさいころ　　→偶然が２つ起こる　　→表を書きます。

　でも突然「表を書け」と言われても困るかも知れませんね。表の書き方を説明しましょう。偶然が２つ起こるので、一方の偶然で起こるすべての場合を縦にします。

もう片方の偶然で起こるすべての場合を横に並べて、

こんな感じの表にします。今回の問題の場合は、大きなさいころの目を縦に、小さなさいころの目を横に並べておきます。どっちがどっちかは、自分で決めていいです。

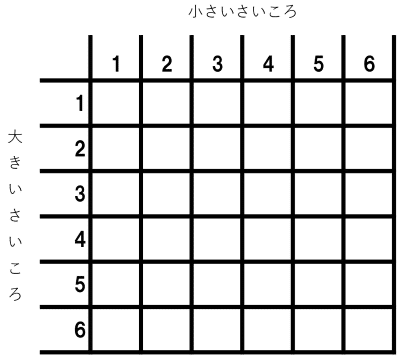
　そうすると、このマス目マス目１つ１つが、

　「大きなさいころで１、小さなさいころで１が出るとき」
　「大きなさいころで１、小さなさいころで２が出るとき」
　「大きなさいころで１、小さなさいころで３が出るとき」
　「大きなさいころで１、小さなさいころで４が出るとき」
　「大きなさいころで１、小さなさいころで５が出るとき」
　「大きなさいころで１、小さなさいころで６が出るとき」
　「大きなさいころで２、小さなさいころで１が出るとき」
　「大きなさいころで２、小さなさいころで２が出るとき」
　「大きなさいころで２、小さなさいころで３が出るとき」
　「大きなさいころで２、小さなさいころで４が出るとき」
　「大きなさいころで２、小さなさいころで５が出るとき」
　「大きなさいころで２、小さなさいころで６が出るとき」
　「大きなさいころで３、小さなさいころで１が出るとき」
　「大きなさいころで３、小さなさいころで２が出るとき」
　「大きなさいころで３、小さなさいころで３が出るとき」
　「大きなさいころで３、小さなさいころで４が出るとき」
　「大きなさいころで３、小さなさいころで５が出るとき」
　「大きなさいころで３、小さなさいころで６が出るとき」
　「大きなさいころで４、小さなさいころで１が出るとき」
　「大きなさいころで４、小さなさいころで２が出るとき」
　「大きなさいころで４、小さなさいころで３が出るとき」
　「大きなさいころで４、小さなさいころで４が出るとき」
　「大きなさいころで４、小さなさいころで５が出るとき」
　「大きなさいころで４、小さなさいころで６が出るとき」
　「大きなさいころで５、小さなさいころで１が出るとき」
　「大きなさいころで５、小さなさいころで２が出るとき」
　「大きなさいころで５、小さなさいころで３が出るとき」
　「大きなさいころで５、小さなさいころで４が出るとき」
　「大きなさいころで５、小さなさいころで５が出るとき」
　「大きなさいころで５、小さなさいころで６が出るとき」
　「大きなさいころで６、小さなさいころで１が出るとき」
　「大きなさいころで６、小さなさいころで２が出るとき」
　「大きなさいころで６、小さなさいころで３が出るとき」
　「大きなさいころで６、小さなさいころで４が出るとき」
　「大きなさいころで６、小さなさいころで５が出るとき」
　「大きなさいころで６、小さなさいころで６が出るとき」

という意味になります。これを書いて並べるのはうっとうしくてしょうがないですね。表にコンパクトにまとめられるので便利だ、というわけです。

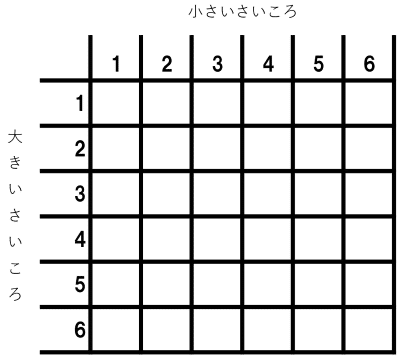
　そして、それぞれのできごとは同じ確率で起こります。同じ確率で起こることを同様に確からしいといいます。確率を求める、ということは、同様に確からしいことを全部並べて、それをくじに見立て、「くじは何本？　その中で当たりは何本？」というのを求めることと同じです。分母はくじの本数ですね。

・・・・というわけで、起こりうるすべての場合の数、くじの本数が分母になるのでした。この問題（というか、大小２つのさいころの場合は）３６ということになります。ちょっと説明が長かったですね。

分子は・・・

　条件に合うのは、

　「大きなさいころで１、小さなさいころで１が出るとき」
　「大きなさいころで２、小さなさいころで２が出るとき」
　「大きなさいころで３、小さなさいころで３が出るとき」
　「大きなさいころで４、小さなさいころで４が出るとき」
　「大きなさいころで５、小さなさいころで５が出るとき」
　「大きなさいころで６、小さなさいころで６が出るとき」

の６通りです。

　こうやっていちいち並べるよりも、せっかく表を書いていますので、条件に合うところに印をつけて、くじの「当たり」にしてしまいましょう。

　表のますめの数が全部のくじの数、○をつけたのが当たりですね。

分子は　６

答え

というわけで、確率の公式に当てはめて答えましょう。

６／３６　＝　１／６

１／６

約分ができるかどうか、最後に確認を忘れないようにしましょうね。

問題を解いた後に・・・偶然が２つ起こるときは表を書く

　今回は、超ていねいに言葉にしたのですが、逆にこうやって言葉にするとまどろっこしい感じもします。でもいったん超ていねいにやって行くと、このあと見失ったときに、ここに戻ってくればいい、というのを考えて、あえて超ていねいにやっておきました。（後で戻ってきて、なるほどと思ってもらってもいいし）

　まとめると、偶然が１つのときは、表を書くまでもありません。そして、３つ以上起こるときは表は使えません。樹形図の方が便利ですが、樹形図の話は基礎編１８以降で触れることにします。

　・・・話が長くなりました。表は別にさいころ２つの問題に限ったことではなく「偶然が２つ起こるとき」の道具としてジャンジャン使えばいいのでというのがこのnoteのメインテーマです。

偶然が２つ起こるとき、表を書く

　じゃあ、偶然が２つ起こる，というのはどういうときか？　それは、偶然を１人１つに分担する，と考えるわけです。

－－－－－－－－－－－－－－－－－－－－－－－
＜前の問題　　　　　次の問題＞
問題一覧

類題

東京都2021、愛知県B2021