埼玉県追試験｜公立高校入試確率問題2022

　数直線上の原点に点Ｐがあり，１から６までの目が出る１つのさいころを投げ，次のルールにしたがって点Ｐを移動させます。さいころを２回投げるとき，次の確率を求めなさい。
　ただしさいころはどの目が出ることも同様に確からしいものとします。
ルール
　１，３，５の目が出たとき，出た目の数だけ正の方向に点Ｐを移動させる。
　２，４，６の目が出たとき，出た目の数の半分だけ負の方向に点Ｐを移動させる。

（１）点Ｐが原点にある確率を求めなさい。
（２）点Ｐと原点との距離が３以下になる確率を求めなさい。

（１）は追試験、（２）は学校選択問題

分類　応用❶（他のものを動かす、すごろく型）

表をかいて、（１）を考えます

　問題文には図は提示されていませんので、イメージをつけるために数直線をまず余白とかにかいてもいいですね。

　そしてさいころ２回なので表をかきます。ルールに基づいて１回の移動で点Ｐがどれだけ移動するのかも書き添えておきます。そうすると、２回分の移動の結果は、２つを足し算すればわかります。

　（１）は、点Ｐが原点にあるということで、移動結果が０になっていればよいわけです。〇印をつけます。

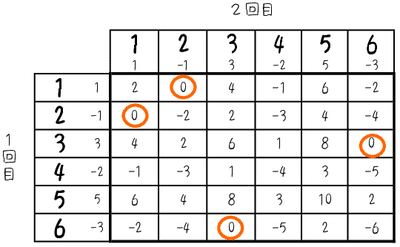
　４通りですので、確率は$${\dfrac{4}{36}=\bm{\dfrac{1}{9}}}$$です。　

表で（２）も考えます。

　（２）は学校選択問題。難しめの問題ということになっているのですが、この問題はそうでもありません。点Ｐと原点との距離が３以下になるのは、表にかいてある数の絶対値が３以下になる場合ですので、✓印をつけて数えます。０もオッケーですね。

　条件に当てはまる場合は２０通りありますので、確率は$${\dfrac{20}{36}=\bm{\dfrac{5}{9}}}$$です。

答

（１）　$${\bm{\dfrac{1}{9}}}$$　　（２）　$${\bm{\dfrac{5}{9}}}$$