神奈川県｜公立高校入試確率問題2017

　片方の面が白，もう片方の面が黒である同じ大きさで平らな円形の石が６個ある。これら６個の石の白と黒の両面には１，２，３，４，５，６の数がそれぞれ１つずつ書かれており，両面に書かれた数は同じである。上の図１は，書かれた数が１と２の石を示しており，１の石は白の面が上に，２の石は黒の面が上になっている。

　これら６個の石が，図２のように，縦３個横２個に並んだます目に，すべて白の面を上にして１個ずつ，左上から１，２，３，４，５，６の順に並べられている。
　大，小２つのさいころを同時に１回投げ，出た目の数によって，次の【操作１】，【操作２】を順に行うこととする。
【操作１】　大きいさいころの出た目の数の約数と同じ数が書かれた石をすべて裏返す。
【操作２】　小さいさいころの出た目の数の約数と同じ数が書かれた石をすべて裏返す。

例
　大きいさいころの出た目の数が１，小さいさいころの出た目の数が４のとき，【操作１】で図２の１が書かれた石を裏返し，【操作２】で１，２，４が書かれた石を裏返す。
　この結果，図３のように，１，３，５，６が書かれた石は白の面が上に，２，４が書かれた石は黒の面が上になっている。

　いま，石が図２のように並べられている状態で，大，小２つのさいころを同時に１回投げるとき，次の問いに答えなさい。ただし，大，小２つのさいころはともに，１から６までのどの目が出ることも同様に確からしいものとする。（※選択肢問題から改題）
（ア）　すべての石の白の面が上となる確率を求めなさい。
（イ）　白の面が上になっているすべての石の，白の面に書かれた数の積が60の倍数となる確率を求めなさい。

分類：応用〈３〉　裏返す

（ア）は

　大・小２つのさいころとも、同じ目が出たときに全ての石の白の面は上になっています。
　しかし「それだけじゃない」かもしれません。他の場合でもそうなるかもしれません。念のため解く時間があるのなら、全部の場合を確かめてみることをおすすめします。
　そうして、この場合は大丈夫，という確認ができます。

　表の書き方も工夫がいると思います。まずは、約数を左に書いておいて、各マスは「黒」になる数を書いておきます。
　大小順序を入れかえても同じ結果になりますので、表の中でも，対角線上と、左上側だけ確かめればオッケーだ、ということも、ちょっと知っておいた方がいいかもしれません。

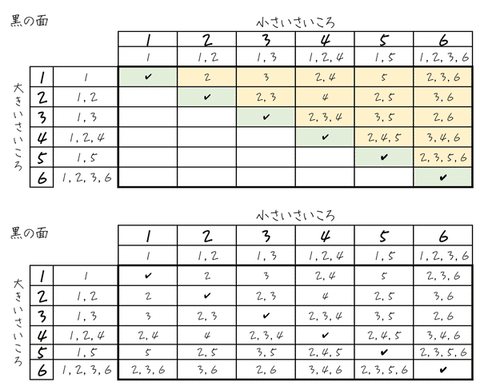
　というわけで、確かに同じ目のときだけ、全ての石の白の面が上になっていることがわかります。

（イ）は

　これは、いくつか考え方がありそうですが，ここではもう一度白で残っているところをもうひとつ表にして，その積を考えることにしましょう。さっきのように、対角線上と左上側だけ計算をして、右下は対角線と対象なところだけ○をすれば、全ての場合を網羅することができます。あと、６０の倍数であるかどうかがわかればいいので、６０がつくれる組合せを見つけることができれば，６０×残り、ということで６０の倍数であることは十分に確かめられます。こうした［ショートカット］を駆使すれば、２枚表をかくことになりますが、手堅く素直な方法で、楽する方法が思いつかない人にとっては手っ取り早いのでは、と考えています。

　あてはまるのは16通り。ですから確率は、$${\dfrac{16}{36}=\bm{\dfrac{4}{9}}}$$。

答

（1）　$${\bm{\dfrac{1}{6}}}$$　　（2）　$${\bm{\dfrac{4}{9}}}$$

問題を解いたあとに・・・

　試験で出たとき、さいころ２つのときは、あまりゴチャゴチャ考えずに，表をまず書いて，何を埋めればいいか，というところに考えを進めて、最後単純に数えあげてしまった方が確実ですね。

　しかし、試験でなければ、いろいろ解法がないか，確かめてみる態度は必要です。どういうやり方が早道か、ほかにもいろいろ考えられると思います。

　たとえば、白の表をあらためて書かないで、黒の面の表で積を計算して、１×２×３×４×５×６＝７２０を割ってもいいです。ただ計算量が多いかな。

　［60の倍数になるのは・・・］という考え方でアプローチしてもいいでしょうね。ちょっと動画も紹介しておきましょう。

　他にもいろいろとアプローチの仕方を考えてもいいでしょう。上の学校を目指そうという人は、引き出しを増やしておくことは大切です。
　そして、大切なのは，人の解答を見て，なるほどそうやるのか，というので終わりにするのではなく，自分の手を動かして解いてみる，ということです。１回わからなかったら，解説を見て、実際自分で解いてみる。それが力をつけるためには必要ですよ。