秋田県｜公立高校入試確率問題2024

　１から６までの目が出るさいころを投げる。ただし，さいころのどの目が出ることも同様に確からしいものとする。
①　このさいころを１回投げて出た目を$${a}$$とする。$${a+3}$$の値が４の倍数になる確率を求めなさい。
②　このさいころを２回投げたとき，１回目に出た目を$${b}$$，２回目に出た目を$${c}$$とする。$${\dfrac{c}{b}}$$の値が整数になる確率を求めなさい。 

分類：１１　さいころ２つ－代入（その１）

①は羅列

　$${a}$$の値は１・２・３・４・５・６のどれかですから，

　　$${a}$$　　　　$${a+3}$$
　　　１　　　　４◎
　　　２　　　　５
　　　３　　　　６
　　　４　　　　７
　　　５　　　　８◎
　　　６　　　　９

で，起こりうるすべての場合は６通りで，そのうち$${a+3}$$の値が４の倍数になるのは◎印をつけた２通りですから，確率を求めると$${\dfrac{2}{6}=\dfrac{1}{3}}$$。

②は表で羅列

　さいころ２つなので，表を使って考えてチェックする方法で考えましょう。それぞれのマスに$${\dfrac{c}{b}}$$の値を入れます。

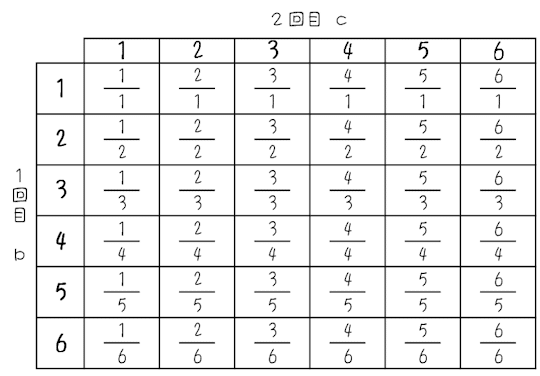
　そのうち約分して整数になるものは

１４通りですから，その確率は$${\dfrac{14}{36}=\dfrac{7}{18}}$$

答

①　$${\bm{\dfrac{1}{3}}}$$　　　②　$${\bm{\dfrac{7}{18}}}$$

スピードアップのために

　②は頻出問題だったりします。分数で考えるとちょっとややこしいです。できるだけ整数のまま考える方がすっきりしますので，「$${\dfrac{c}{b}}$$の値が整数」ということは「$${c}$$が$${b}$$の倍数」と読みえ得た方がいいかもしれません。そうすると，順番に考えれば，表までかかなくても，すべての場合をもれなくダブりなく列挙できますね。

$${b=1}$$のとき　→　$${c=1，c=2，c=3，c=4，c=5，c=6}$$　の６通り
$${b=2}$$のとき　→　$${c=2，c=4，c=6}$$　　の３通り
$${b=3}$$のとき　→　$${c=3，c=6}$$　　の２通り
$${b=4}$$のとき　→　$${c=4}$$　　の１通り
$${b=5}$$のとき　→　$${c=5}$$　　の１通り
$${b=6}$$のとき　→　$${c=6}$$　　の１通り
　あわせて１４通り。